MGEM

MGEM

Finite Difference 3D EM Modelling

• Finite Difference Equation
• The Staggered Grid
• Boundary Conditions
• Multigrid Solver

MGEM

Results and Case Studies

• Synthetic Sphere
• Voisey's Bay Ovoid
• Mystery Project

Equation to Solve

$ (\vec{\nabla} \times \color{orange}{\rho} \vec{\nabla} \times \color{fuchsia}{\vec{\mathrm{H}}}) + \frac{\partial\mu_0\color{fuchsia}{\vec{\mathrm{H}}}}{\partial t} = -\frac{\partial\vec{\mathrm{B}}_p}{\partial t} $

Time Stepping

$ \vec{\mathrm{H}}_i = \vec{\mathrm{H}}_{i-1} + \vec{\mathrm{D}} $

Maxwell's Equations

$ \vec{\nabla} \bullet \vec{\mathrm{E}} = \frac{\rho}{\varepsilon_0} $

$ \vec{\nabla} \bullet \vec{\mathrm{B}} = 0 $

$ \vec{\nabla} \times \vec{\mathrm{E}} = -\frac{\partial\vec{\mathrm{B}}}{\partial t} $

$ \vec{\nabla} \times \vec{\mathrm{B}} = \mu_0 \left(\vec{\mathrm{J}} + \varepsilon_0\frac{\partial\vec{\mathrm{E}}}{\partial t}\right) $

Current Density

$ \color{red}{\vec{\mathrm{E}}} = \color{orange}{\rho}\vec{\mathrm{J}} $

Faraday's Law

$ \vec{\nabla} \times \color{red}{\vec{\mathrm{E}}} = -\frac{\partial\vec{\mathrm{B}}}{\partial t} $

Ampere's Law

$ \vec{\nabla} \times \vec{\mathrm{B}} = \mu_0 \vec{\mathrm{J}} $

Current Density

$ \color{grey}{\vec{\mathrm{E}} = \rho\vec{\mathrm{J}}} $

Faraday's Law

$ \vec{\nabla} \times \color{orange}{\rho}\vec{\mathrm{J}} = -\frac{\partial\vec{\mathrm{B}}}{\partial t} $

Ampere's Law

$ \vec{\nabla} \times \vec{\mathrm{B}} = \mu_0 \vec{\mathrm{J}} $

Current Density

$ \color{grey}{\vec{\mathrm{E}} = \rho\vec{\mathrm{J}}} $

Faraday's Law

$ \vec{\nabla} \times \color{orange}{\rho}\vec{\mathrm{J}} = -\frac{\partial\vec{\mathrm{B}}}{\partial t} $

Ampere's Law

$ \vec{\nabla} \times \color{fuchsia}{\vec{\mathrm{B}}} = \color{fuchsia}{\mu_0} \vec{\mathrm{J}} $

Current Density

$ \color{grey}{\vec{\mathrm{E}} = \rho\vec{\mathrm{J}}} $

Faraday's Law

$ \vec{\nabla} \times \color{orange}{\rho}\color{green}{\vec{\mathrm{J}}} = -\frac{\partial\vec{\mathrm{B}}}{\partial t} $

Ampere's Law

$ \vec{\nabla} \times \color{fuchsia}{\vec{\mathrm{H}}} = \color{green}{\vec{\mathrm{J}}} $

Current Density

$ \color{grey}{\vec{\mathrm{E}} = \rho\vec{\mathrm{J}}} $

Faraday's Law

$ \vec{\nabla} \times \color{orange}{\rho} \vec{\nabla} \times \color{fuchsia}{\vec{\mathrm{H}}} = -\frac{\partial\vec{\mathrm{B}}}{\partial t} $

Ampere's Law

$ \color{grey}{\vec{\nabla} \times \vec{\mathrm{H}} = \vec{\mathrm{J}}} $

Ampere's Law $\longrightarrow$ Faraday's Law

$ \vec{\nabla} \times \color{orange}{\rho} (\vec{\nabla} \times \color{fuchsia}{\vec{\mathrm{H}}}) = -\frac{\partial\vec{\mathrm{B}}}{\partial t} $

Secondary Primary Field

$ \vec{\nabla} \times \color{orange}{\rho} (\vec{\nabla} \times \color{fuchsia}{\vec{\mathrm{H}}}) = \left( \frac{\partial\mu_0\color{fuchsia}{\vec{\mathrm{H}}}}{\partial t} - \frac{\partial\vec{\mathrm{B}}_p}{\partial t} \right) $

Equation to Solve

$ (\vec{\nabla} \times \color{orange}{\rho} \vec{\nabla} \times \color{fuchsia}{\vec{\mathrm{H}}}) + \frac{\partial\mu_0\color{fuchsia}{\vec{\mathrm{H}}}}{\partial t} = -\frac{\partial\vec{\mathrm{B}}_p}{\partial t} $

Time Stepping

$ \color{fuchsia}{\vec{\mathrm{H}}}_i = \color{fuchsia}{\vec{\mathrm{H}}}_{i-1} + \color{fuchsia}{\vec{\mathrm{D}}} $

Finite Difference Equaton

$ \vec{\nabla} \times \color{orange}{\rho} \vec{\nabla} \times \vec{\alpha}\color{fuchsia}{\vec{\mathrm{D}}} + \frac{\mu_0\color{fuchsia}{\vec{\mathrm{D}}}}{h_t} = -\frac{\partial\vec{\mathrm{B}}_p}{\partial t} - \vec{\nabla} \times \color{orange}{\rho}\vec{\nabla} \times\color{fuchsia}{\vec{\mathrm{H}}} $

The Staggered Grid

H-Field

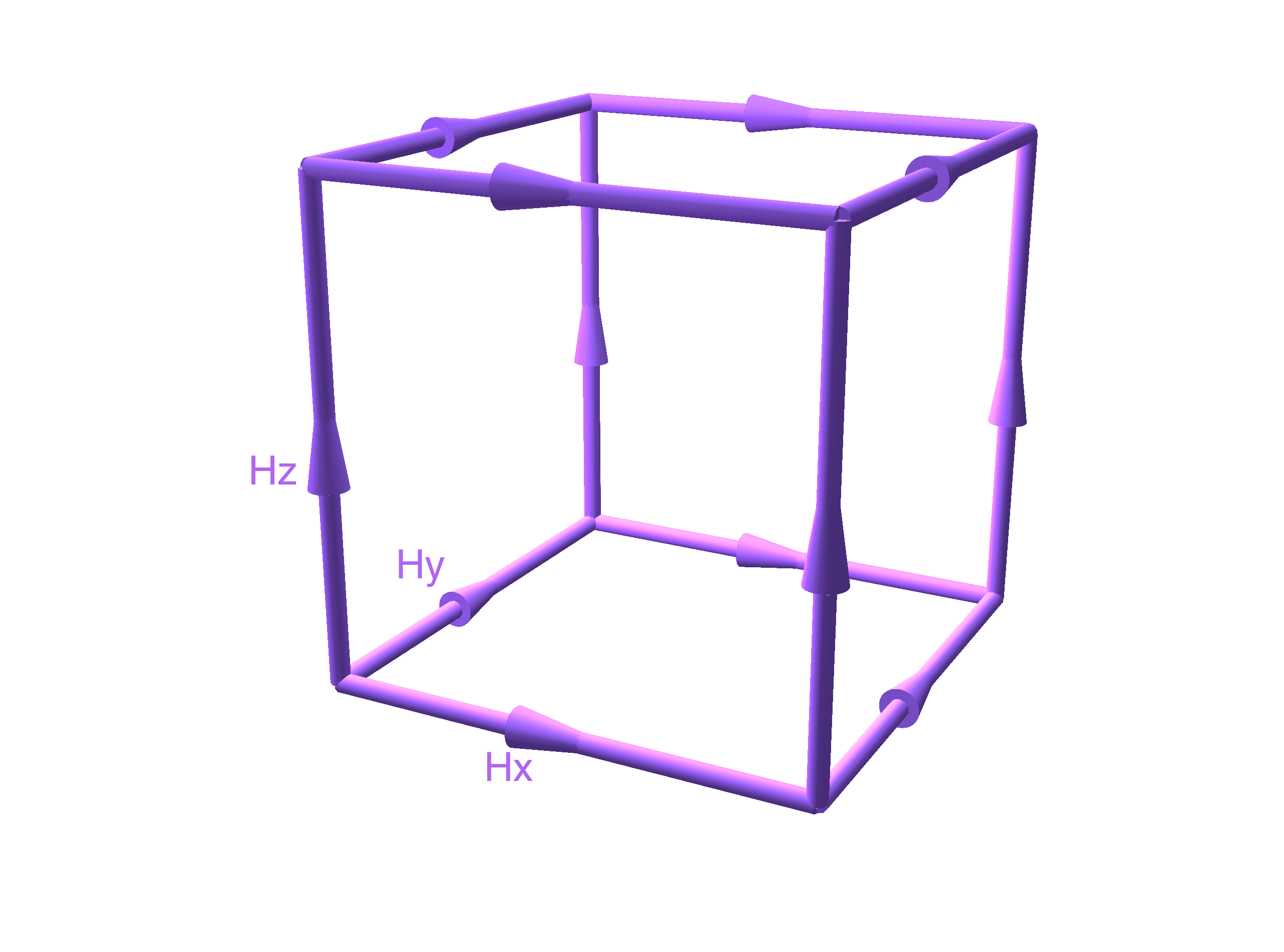
E-Field

Conductivity Subgrid

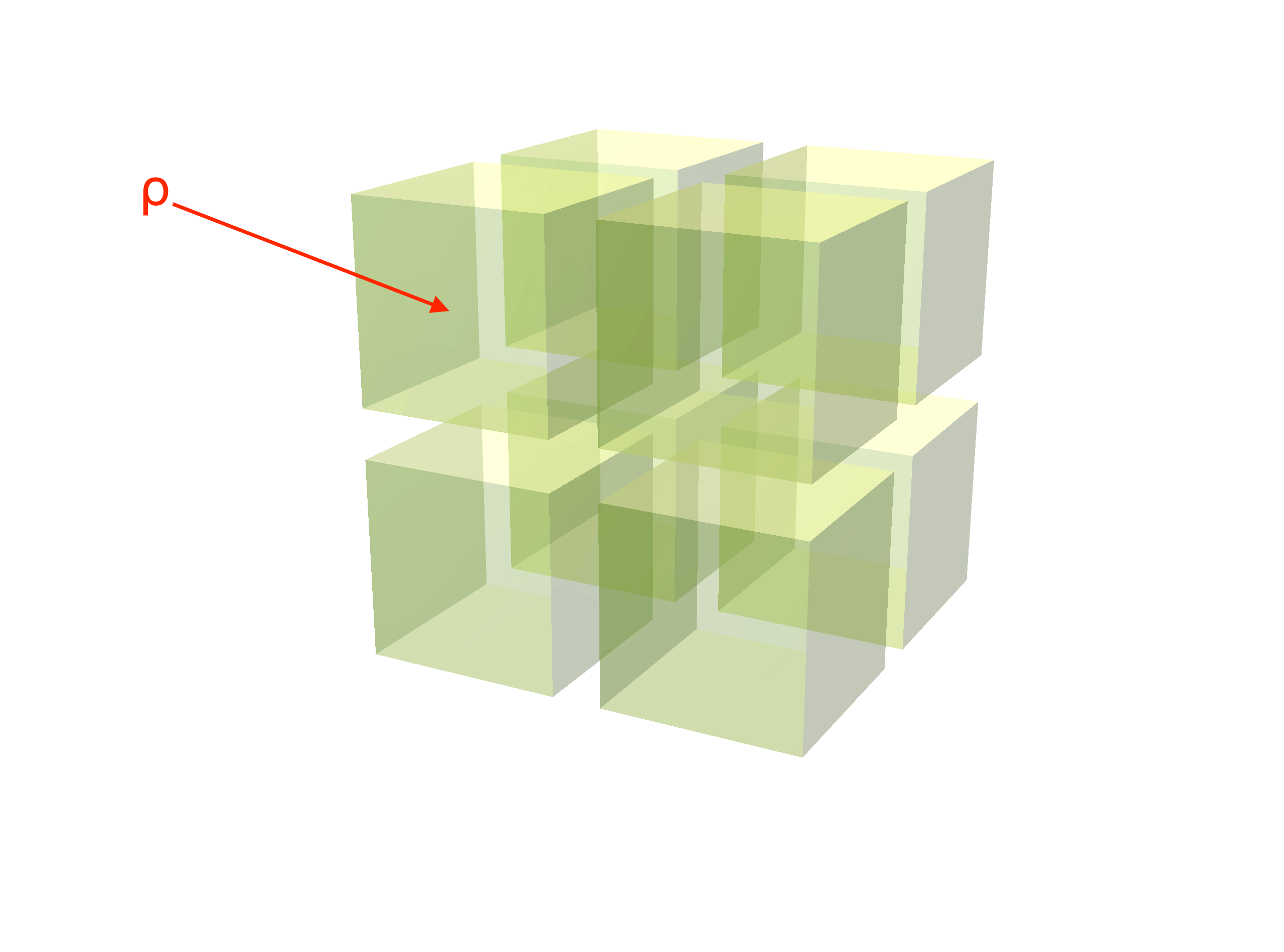
Conductivity Subgrid

Current Density

Current Density

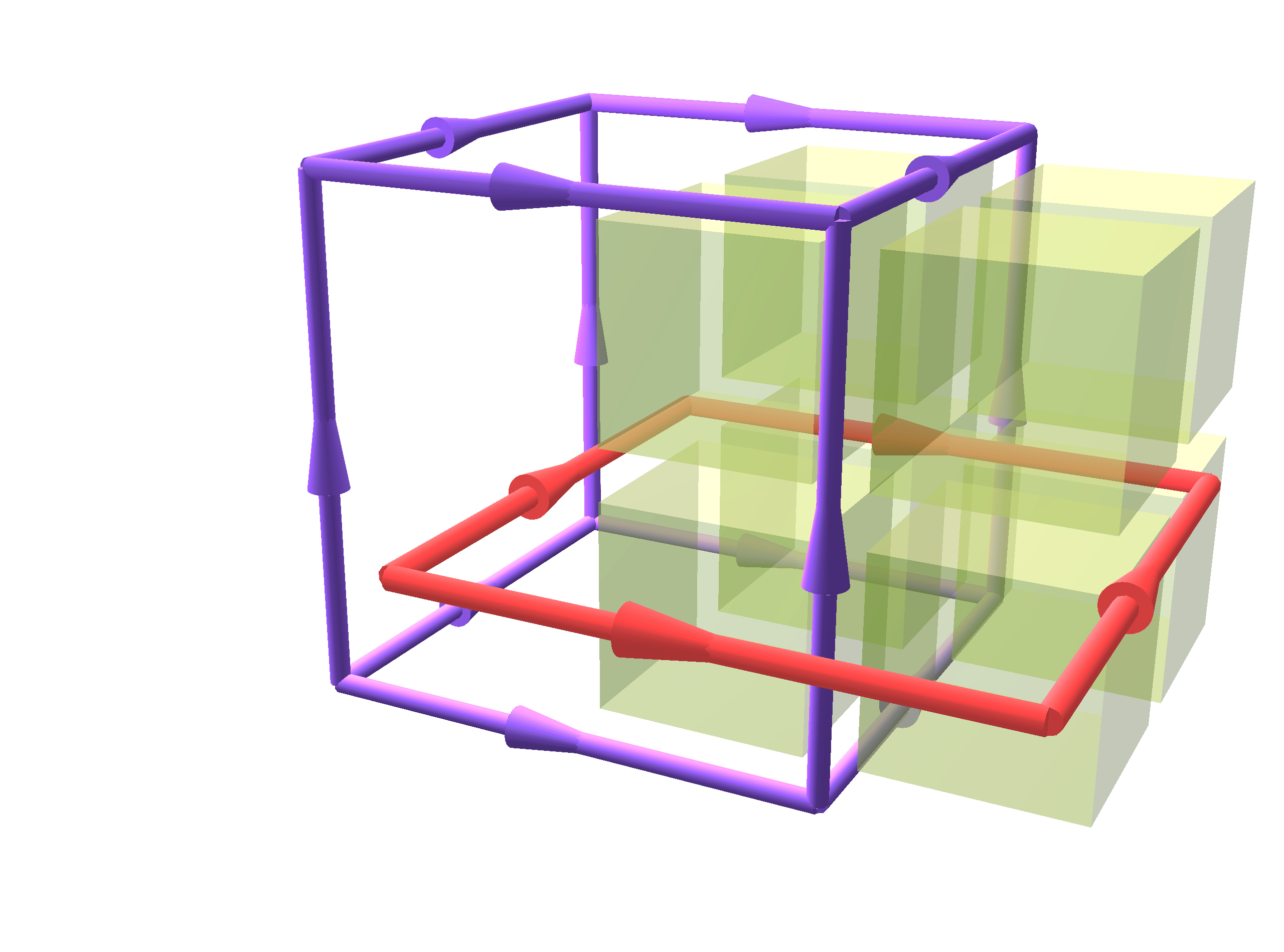
The Staggered Grid

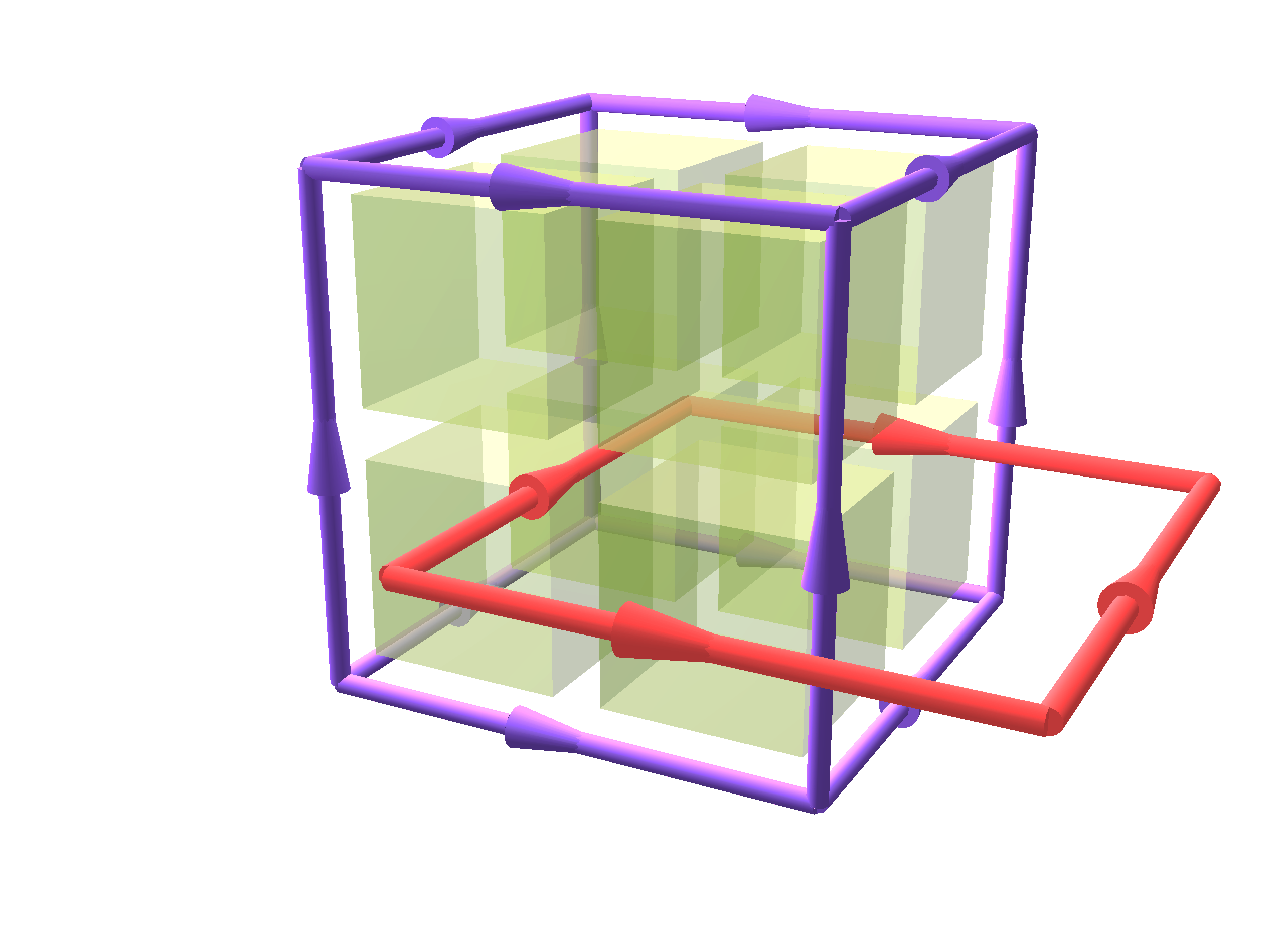
Boundary Conditions

Suitable Initial and Boundary Condition

• $\vec{\mathrm{C}}$ and $\vec{\mathrm{J}}$ start at zero
• $\vec{\mathrm{C}}$ steps on at $t=0$
• $\vec{\mathrm{C}}$ and $\vec{\mathrm{J}}$ decay to zero at infinity

Zero Divergence: The $ \vec{\mathrm{C}} $ Vector

$ \vec{\mathrm{H}} = \vec{\mathrm{C}} - \vec{\nabla}\mathrm{g} $

$ \vec{\mathrm{H}} \longrightarrow \vec{\mathrm{C}} $ provided that $ \vec{\nabla} \bullet \vec{\mathrm{H}} = 0 $

Below Surface

H-Field

C-Field Below Surface

in Free air

$ \vec{\mathrm{H}} = \vec{\nabla}\mathrm{g} $

at surface

$\vec{\mathrm{H}} = \vec{\mathrm{C}} - \vec{\nabla}\mathrm{g} $

below surface

$\vec{\mathrm{H}} = \vec{\mathrm{C}}$

Outer Edge

$\vec{\mathrm{H}_t} = 0$

Outer boundary can be pushed kilometers away

Multigrid Solver

• Speeds up iteration time
• Boundary conditions pushed far from area of interest
• V and W cycle iterations: Interpolation and Sampling

Sphere Test (r = 100 m)

MGEM Software Components

• Gridplot
• 3D Viewer
• MGEM Engine

Model Specifications

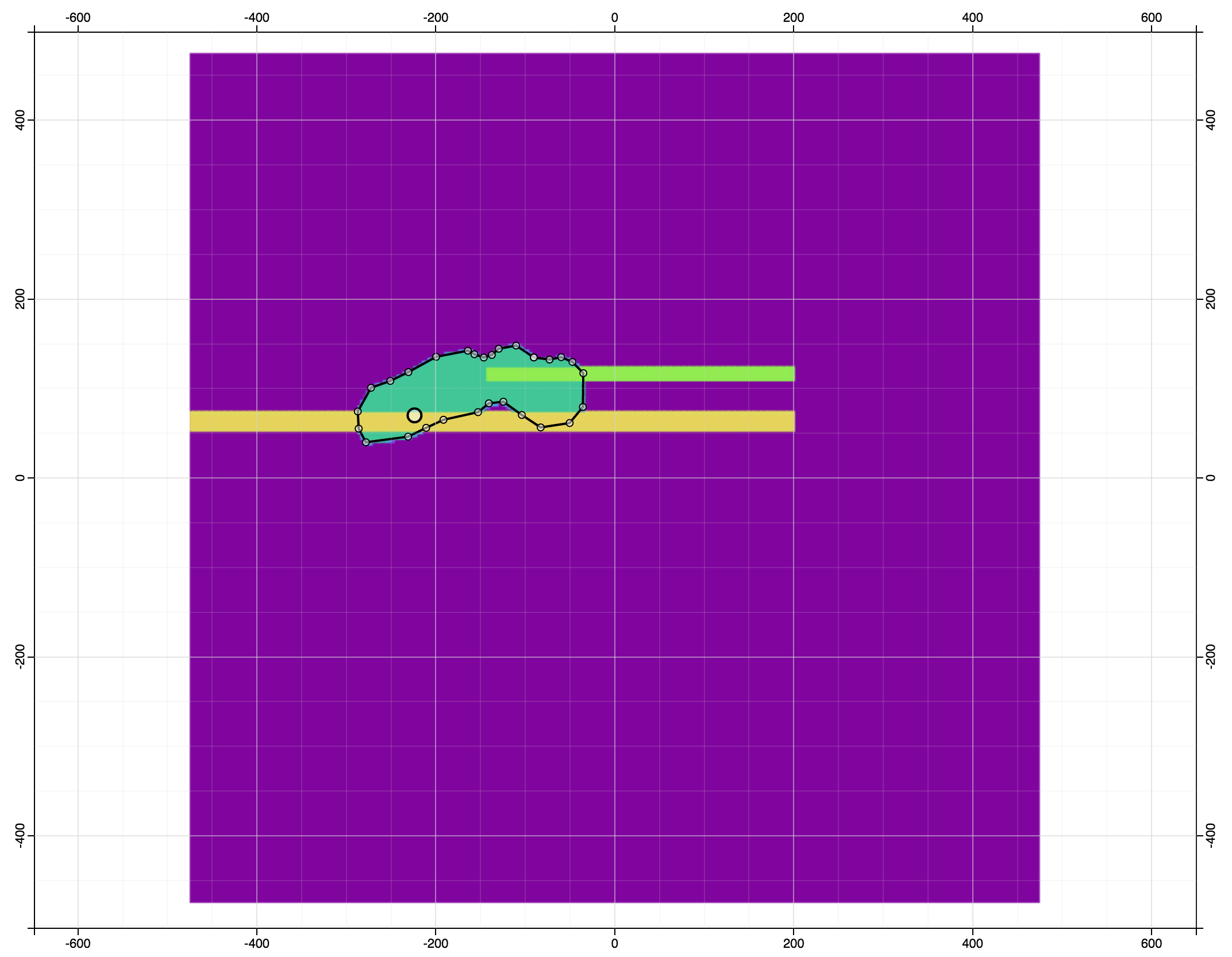
follow the law of geologic superposition

Grid Plot

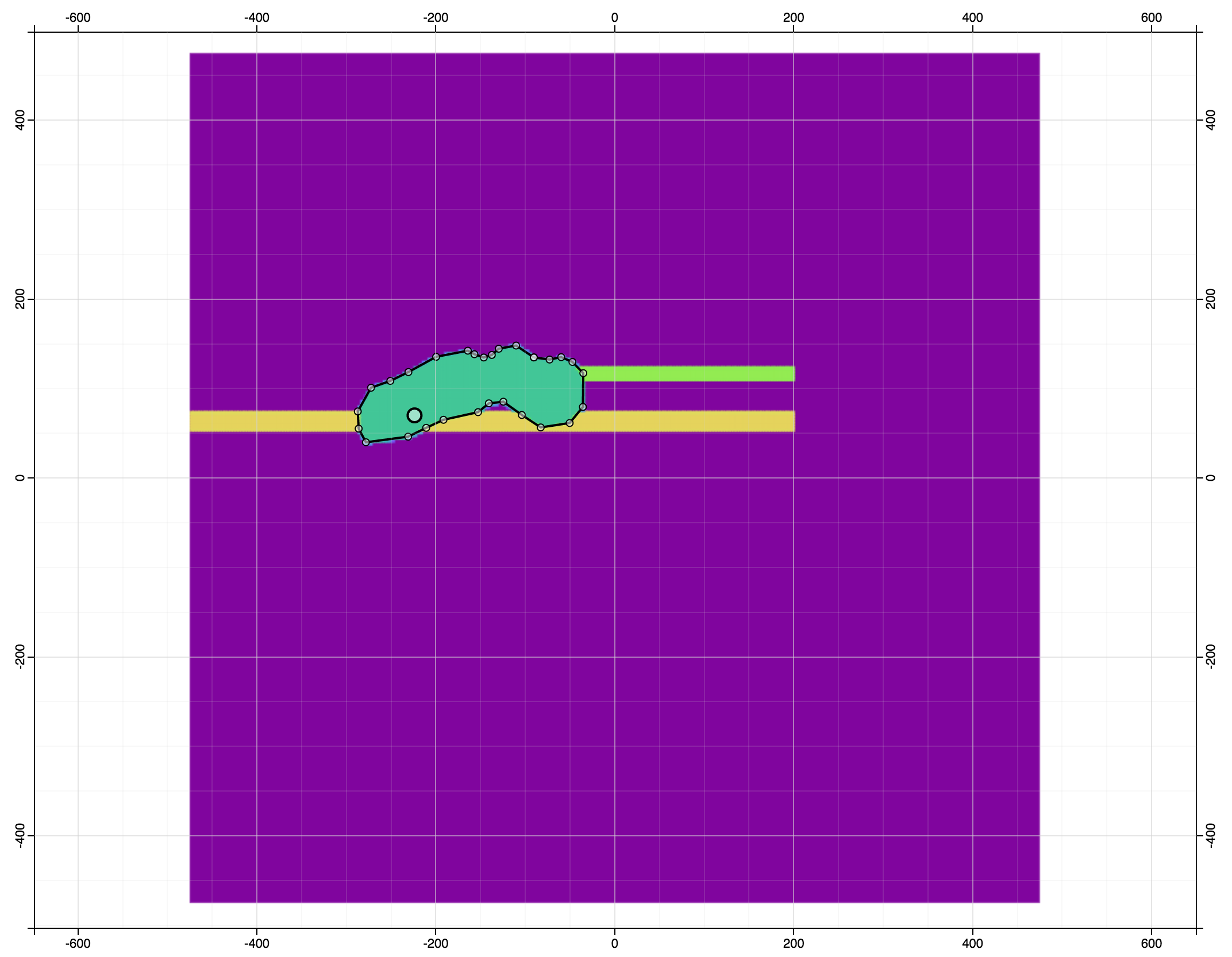
superposition

paths

3D Viewer

MGEM Engine

Four runs at once

Composing Models

• background resistivity
• cuboids
• ellipsoids
• polygonal prisms

Cuboids

• dipping layered earths
• quarter space
• overburden
• conductive or resistive dykes

Ellipsoids

ideal for lenses

Polygonal Prisms

detailing known bodies

All together now

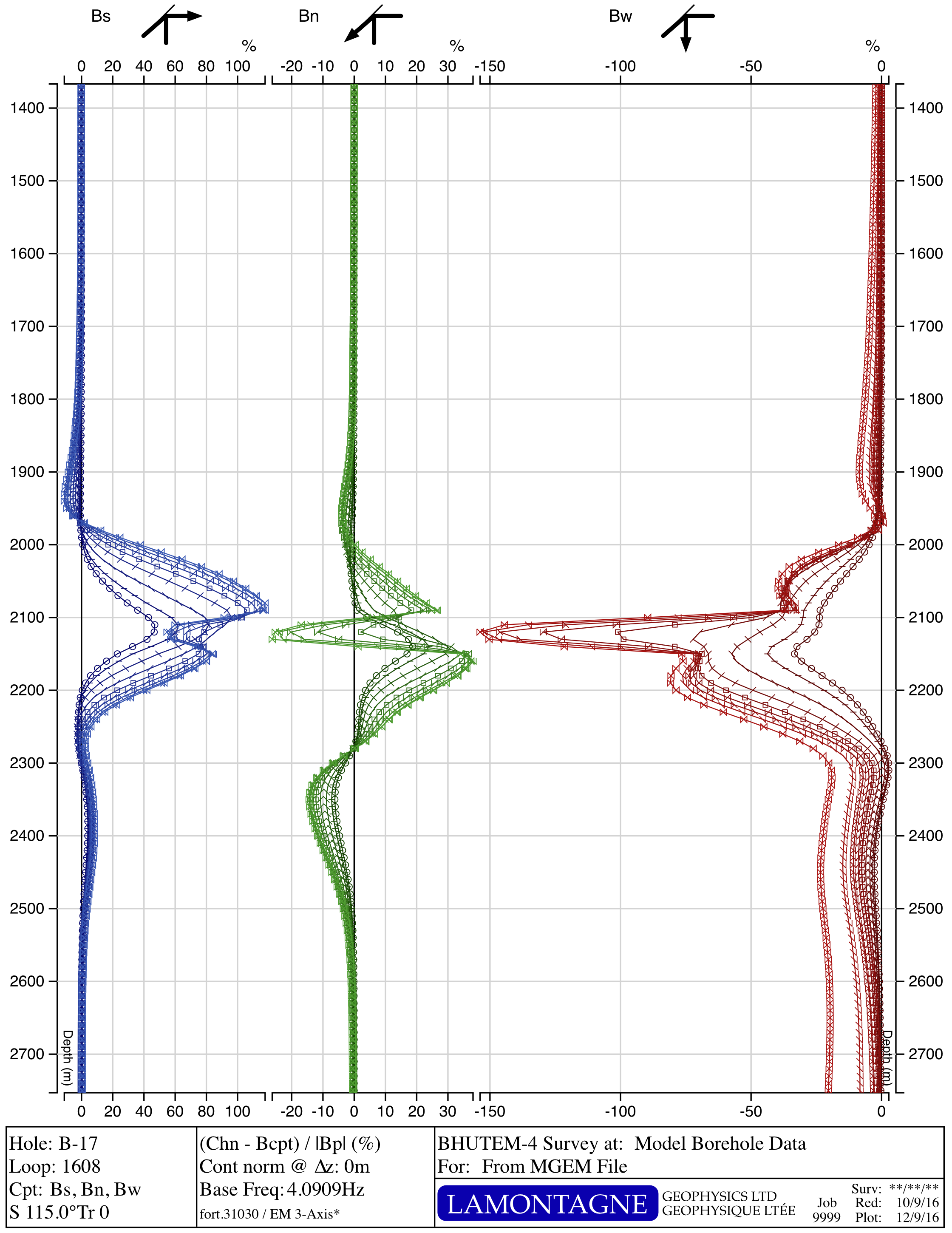
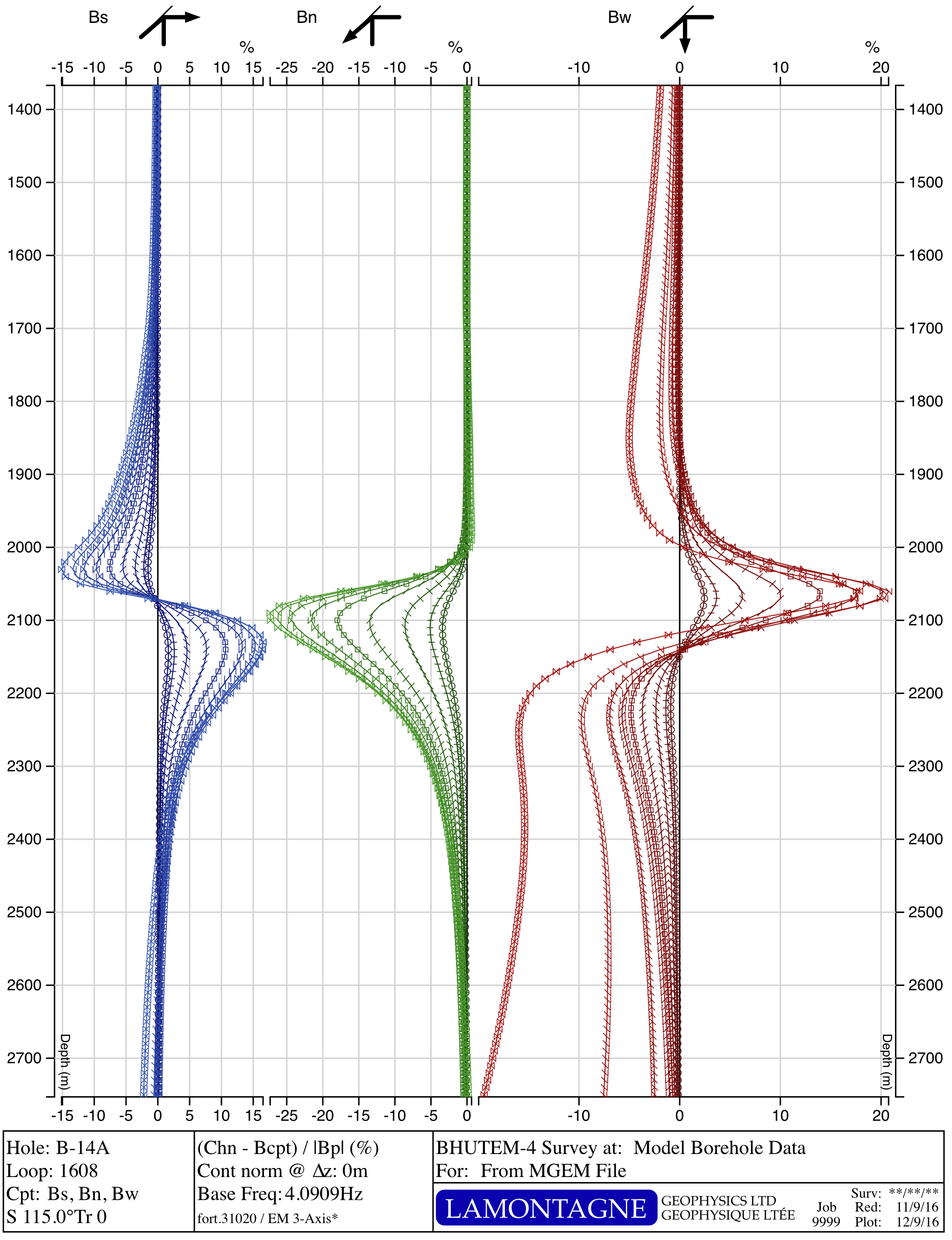
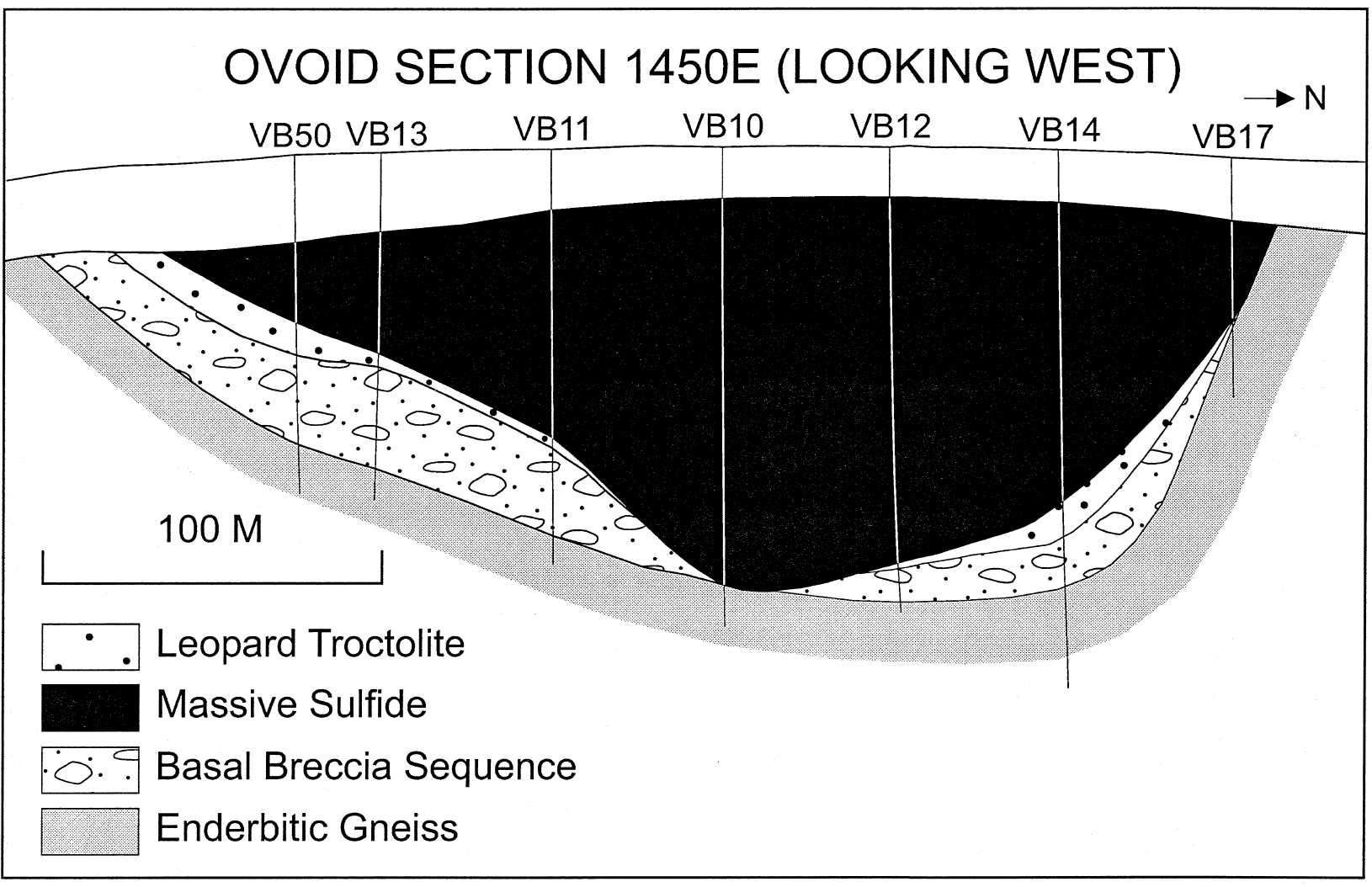
Voisey's Bay Ovoid

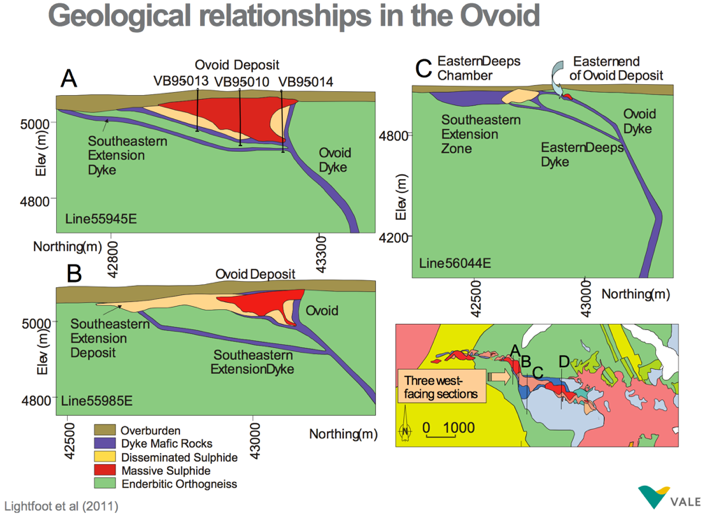
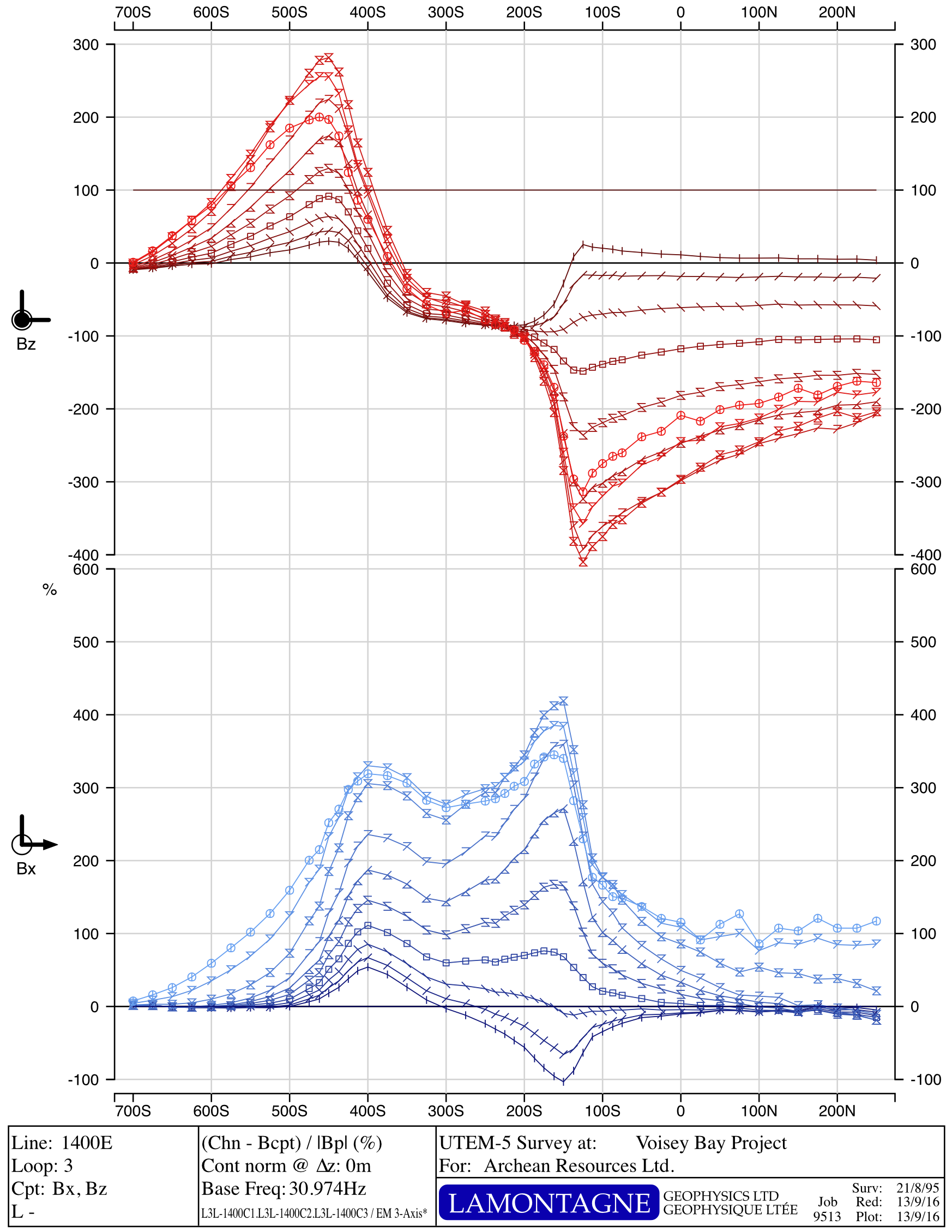
Iterative Forward Modelling

• Ovoid Only
• Overburden
• Troctolyte Dykes
• Conductive Conduit

Ovoid Image Source

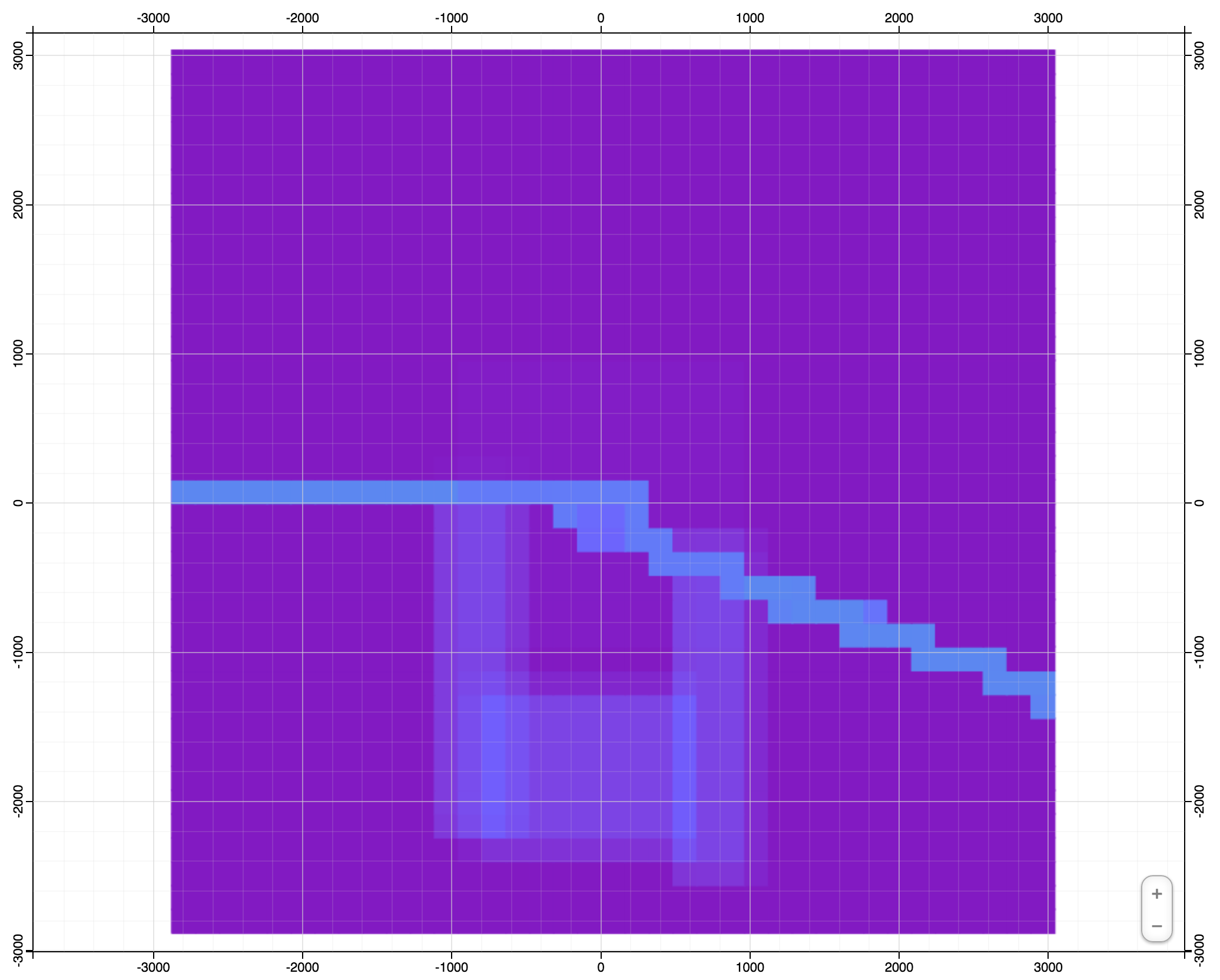
Gridplot Overlay

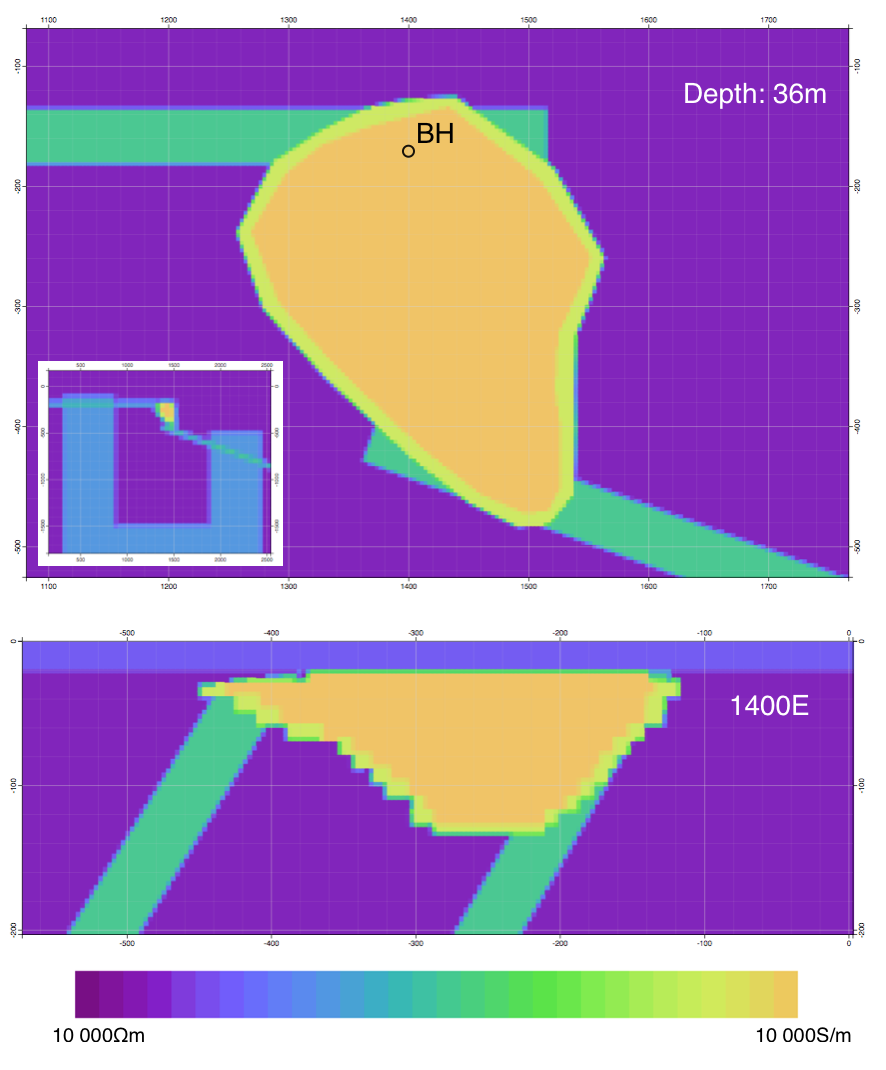
Ovoid X-Section

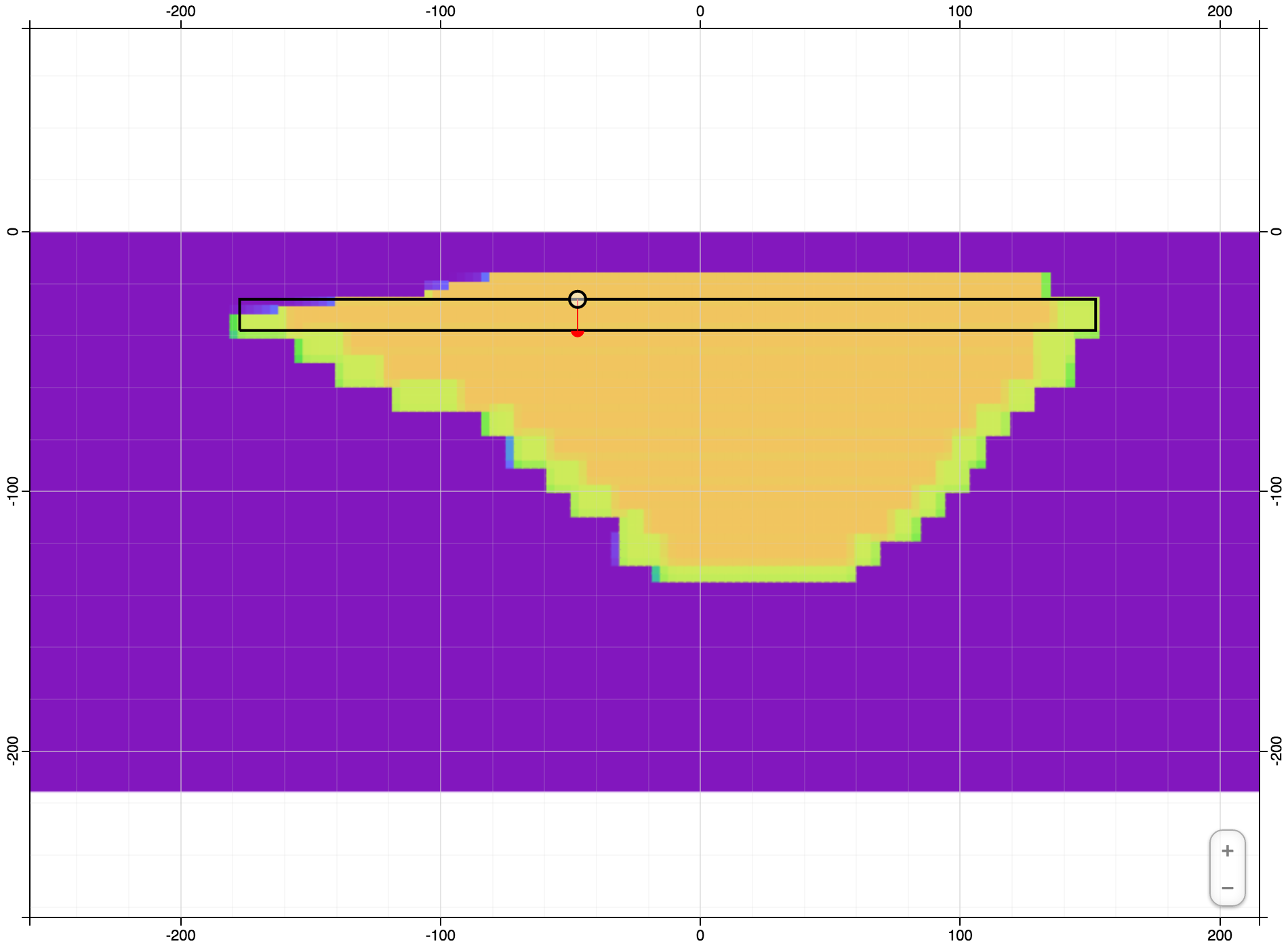
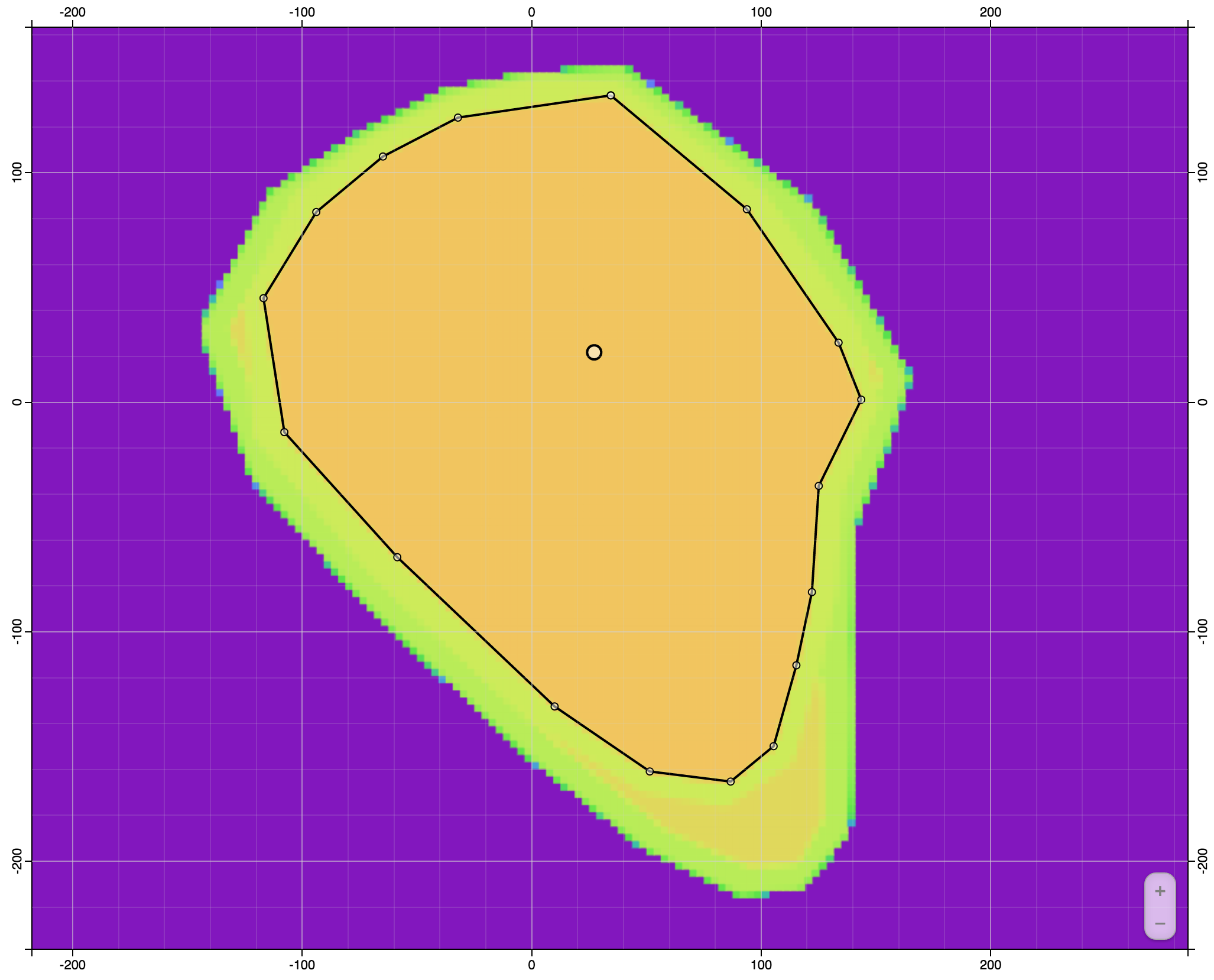
Ovoid Z-Section

Adding OverBurden

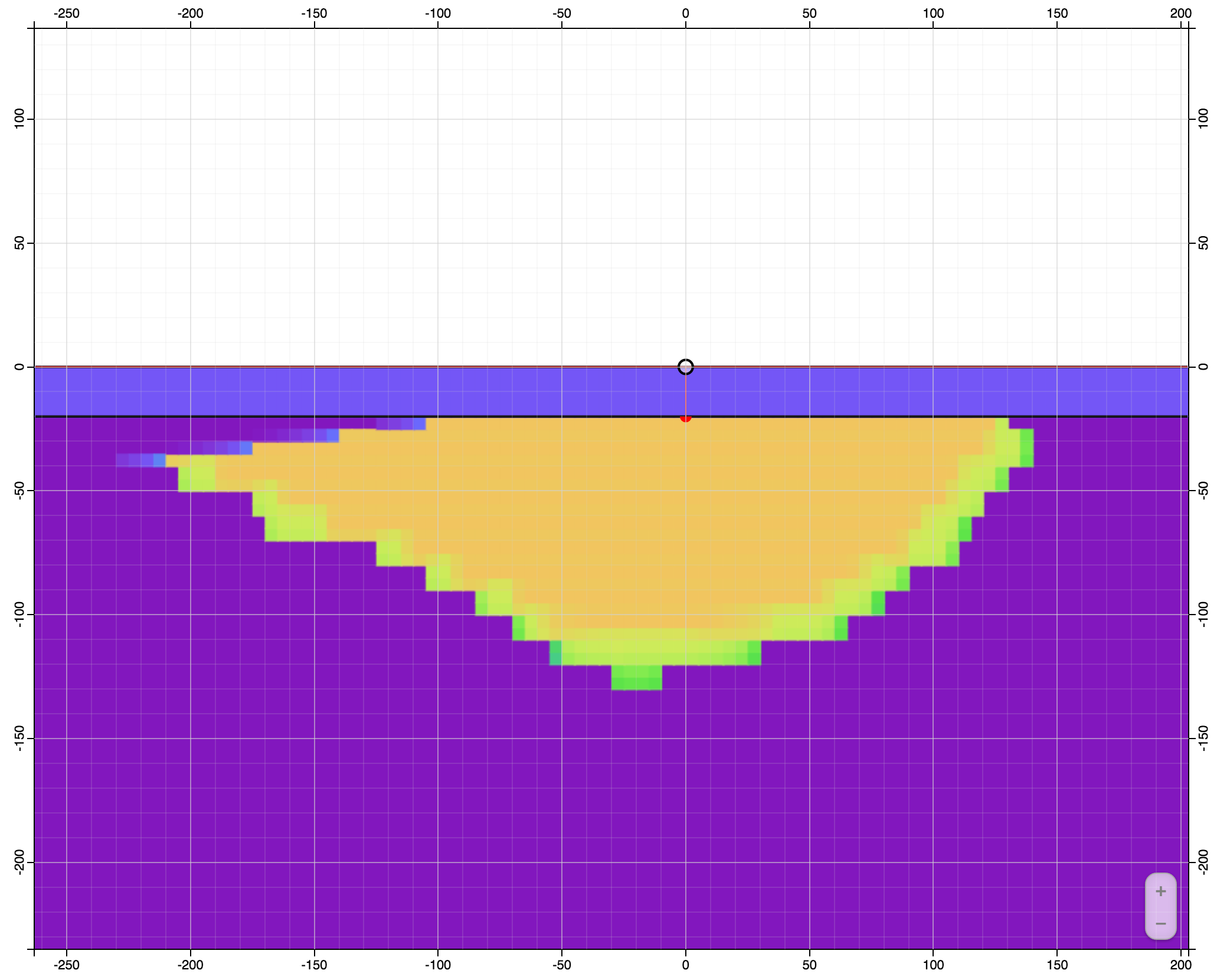
Troctolyte Dykes - Level 1

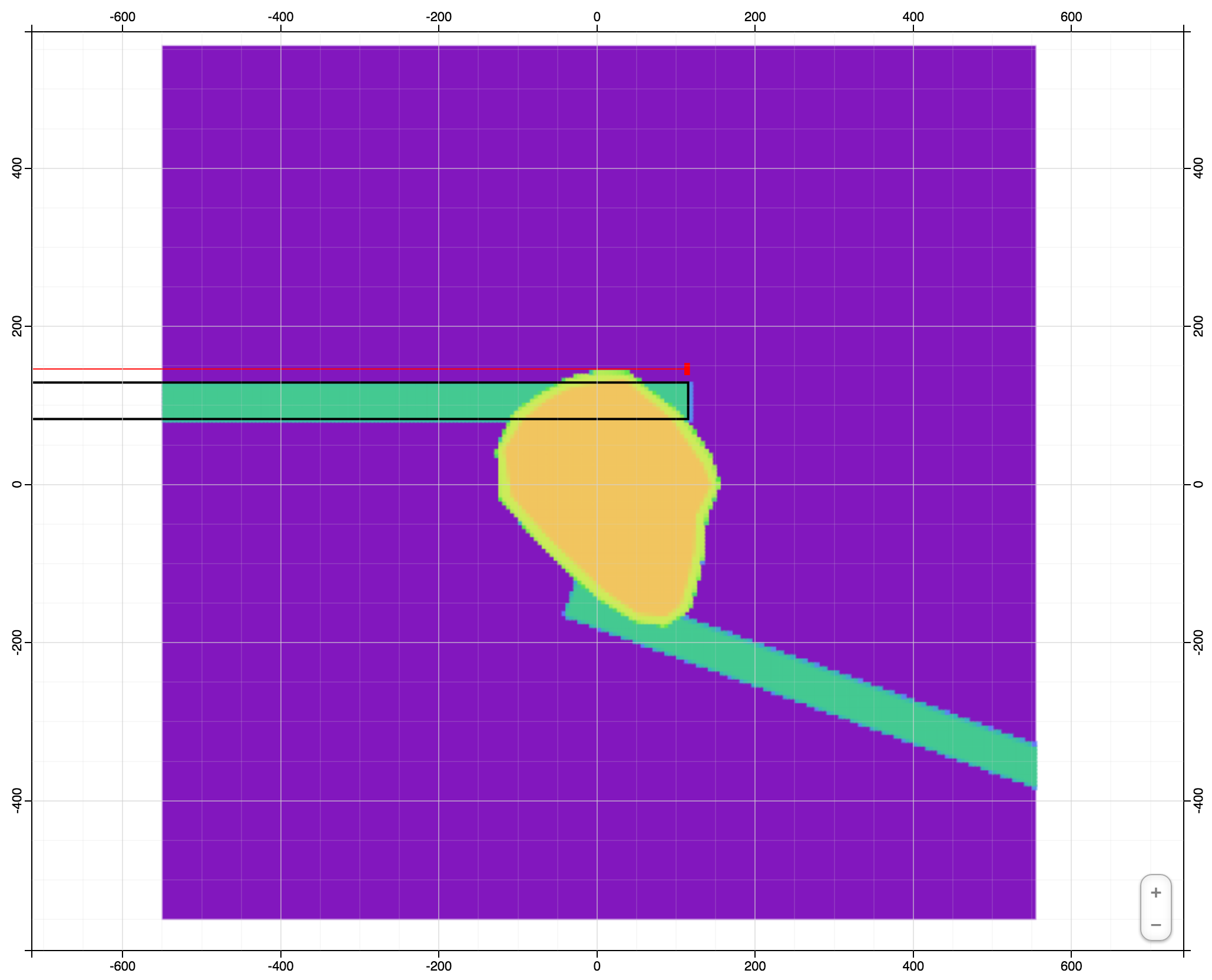
Troctolyte Dykes - Level 3

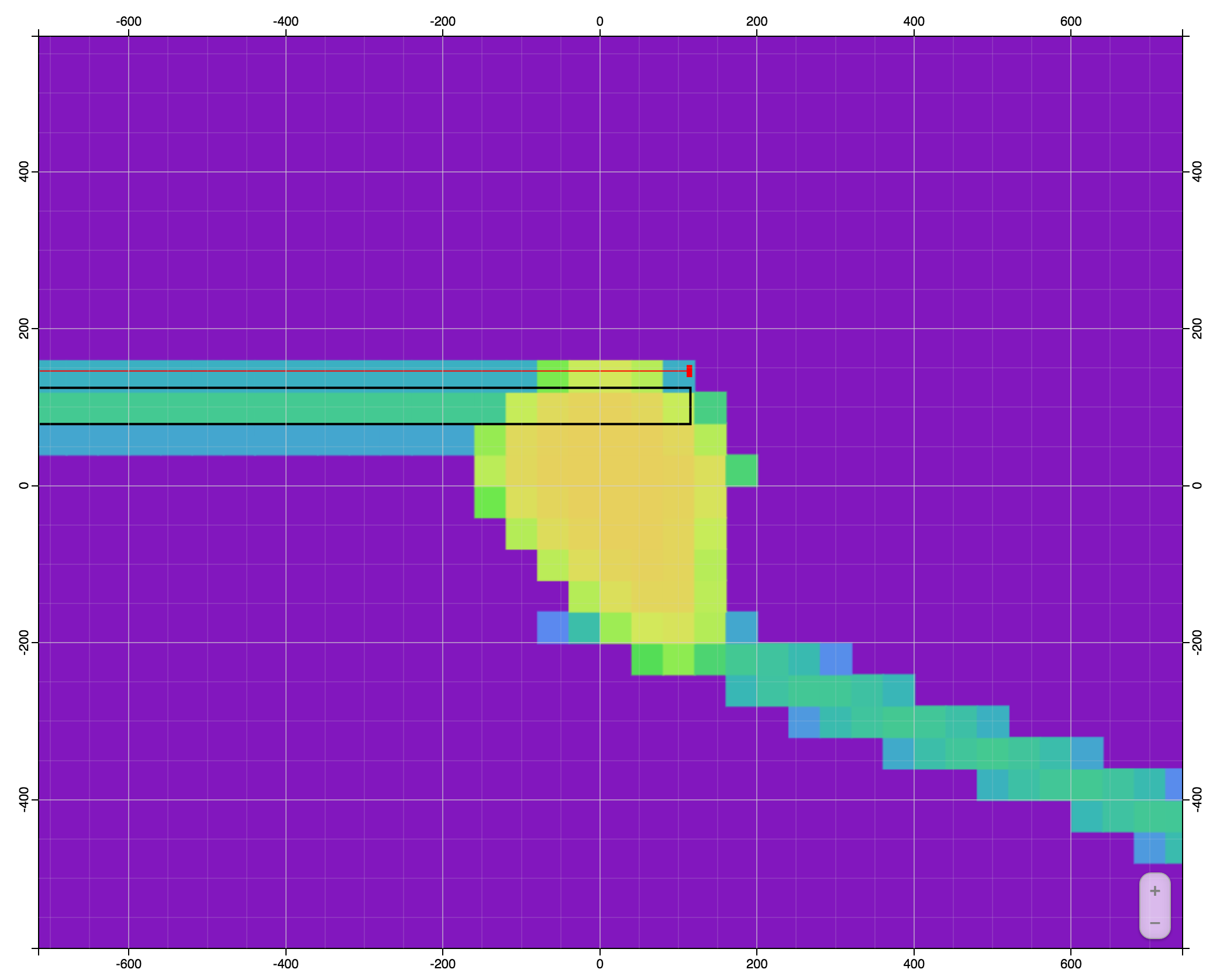
Troctolyte Dykes - Level 6

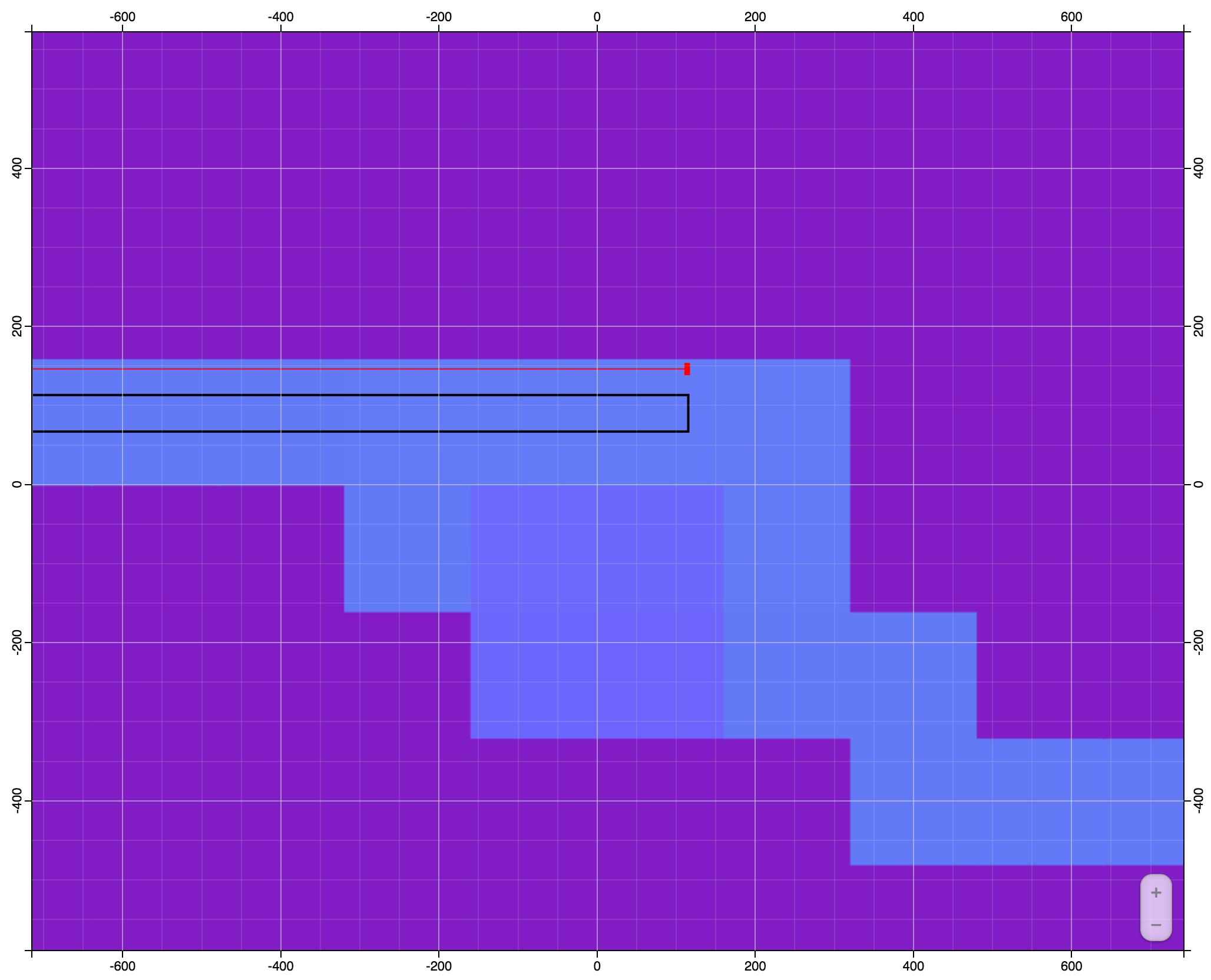
Adding a Conduit at Depth

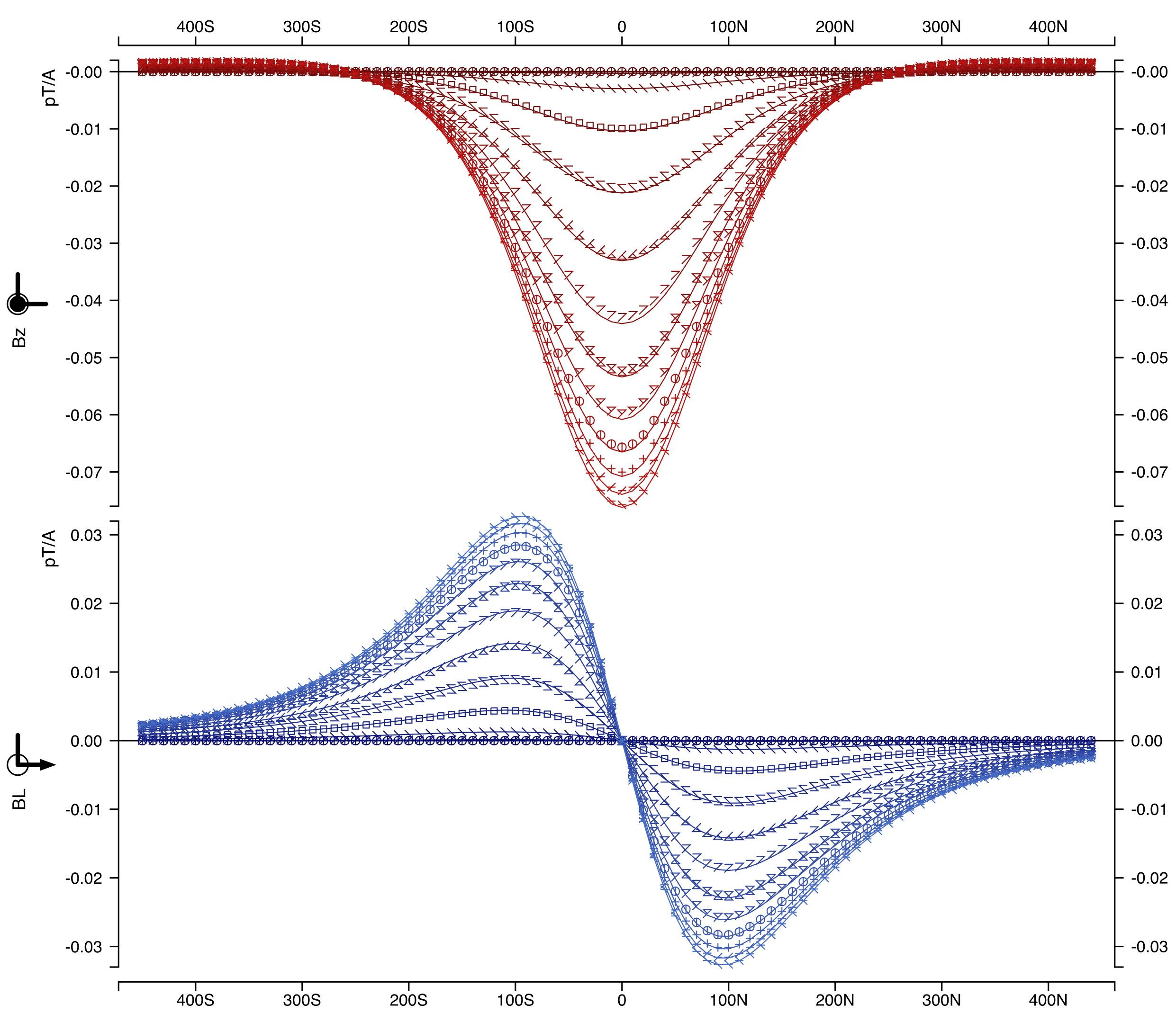
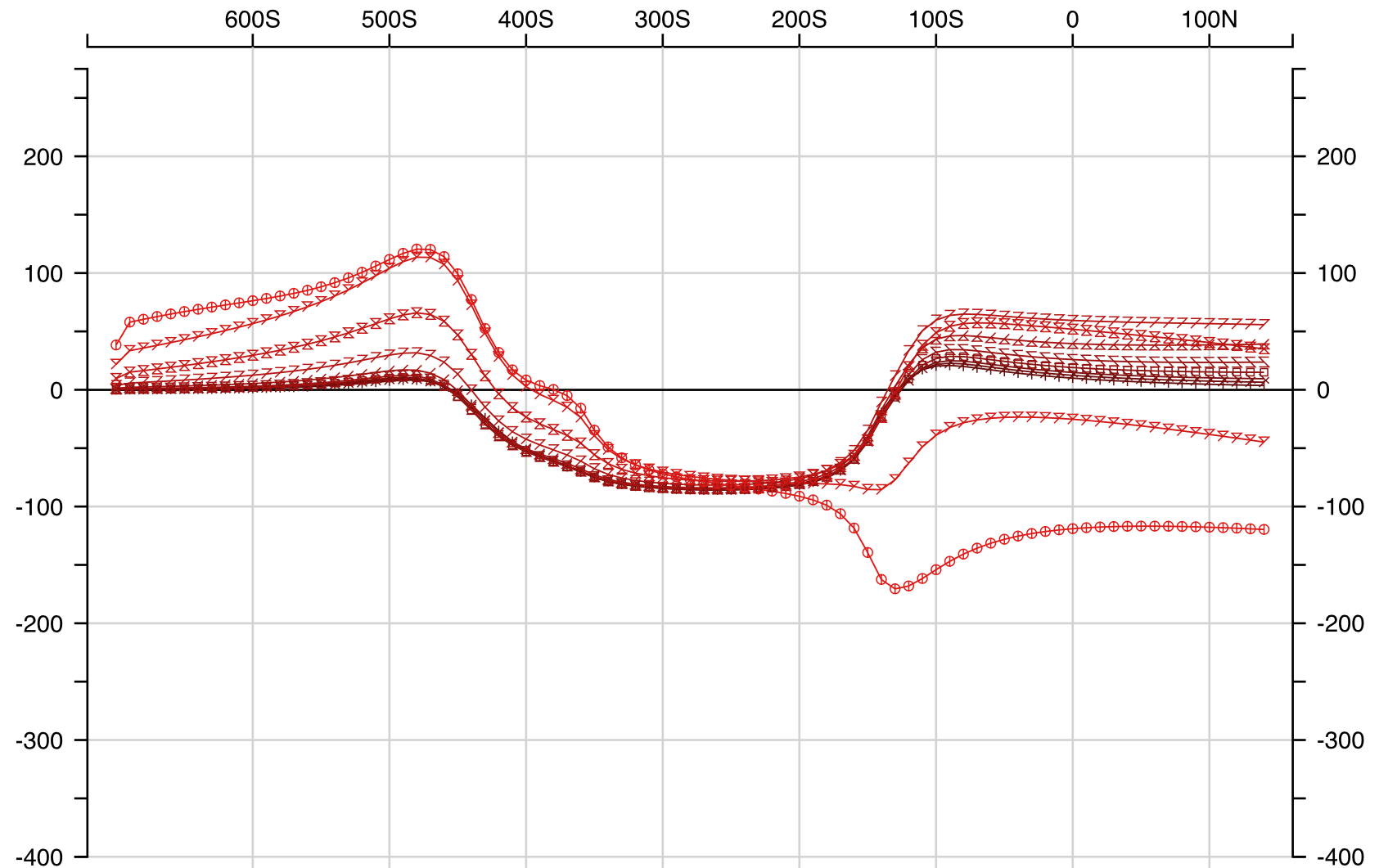
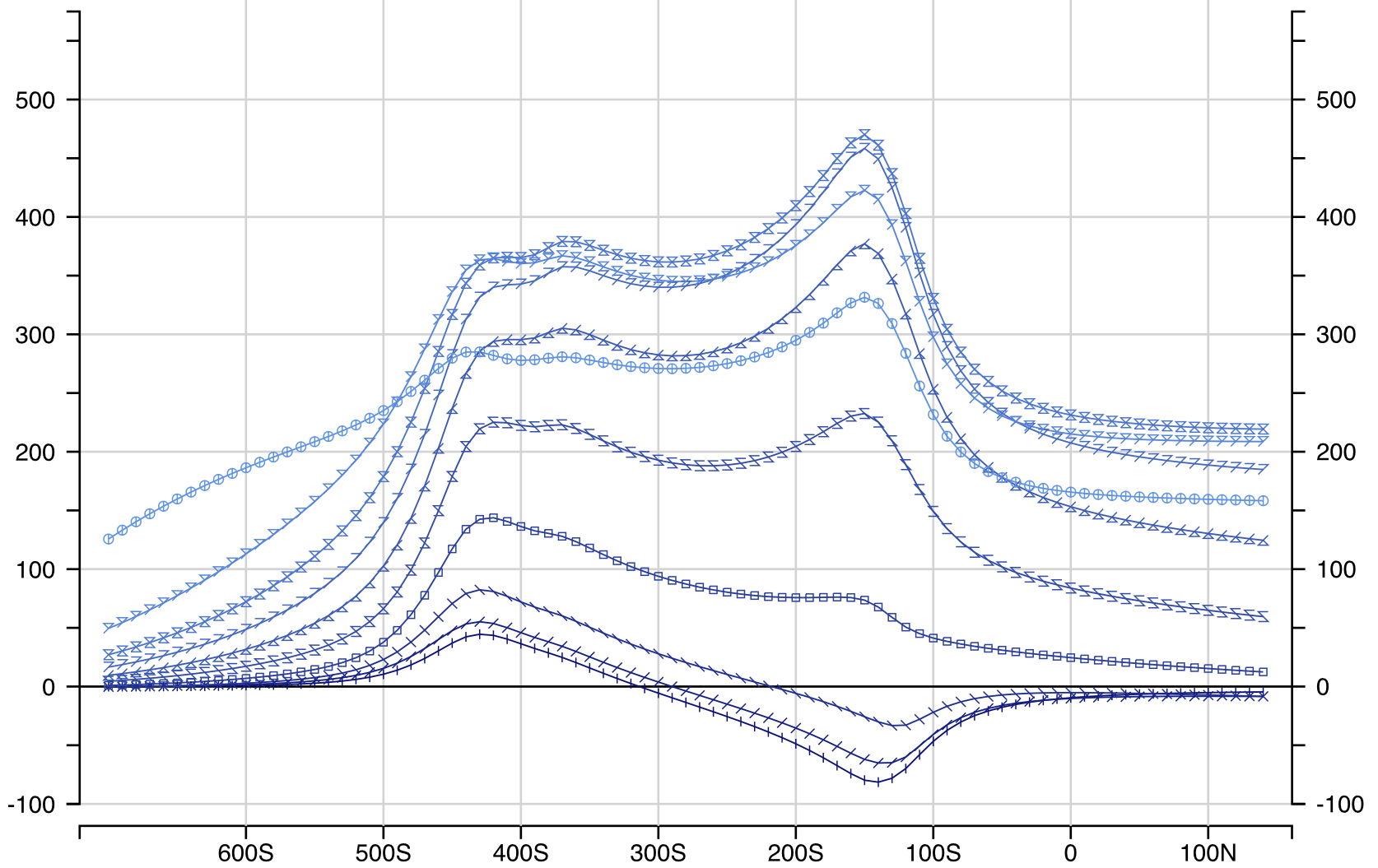
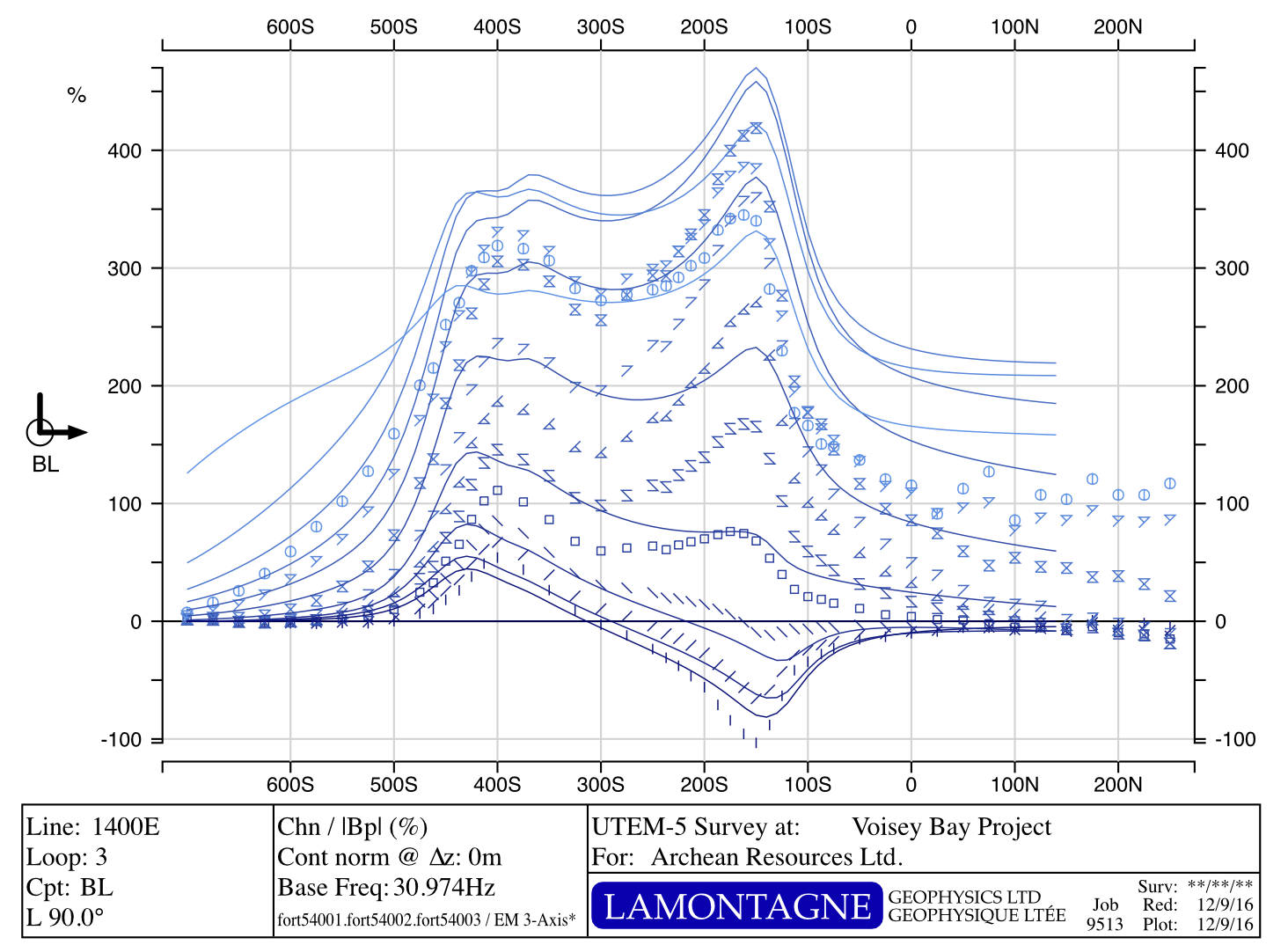
Ovoid + OverBurden Hz

Ovoid + OverBurden + Dykes Hz

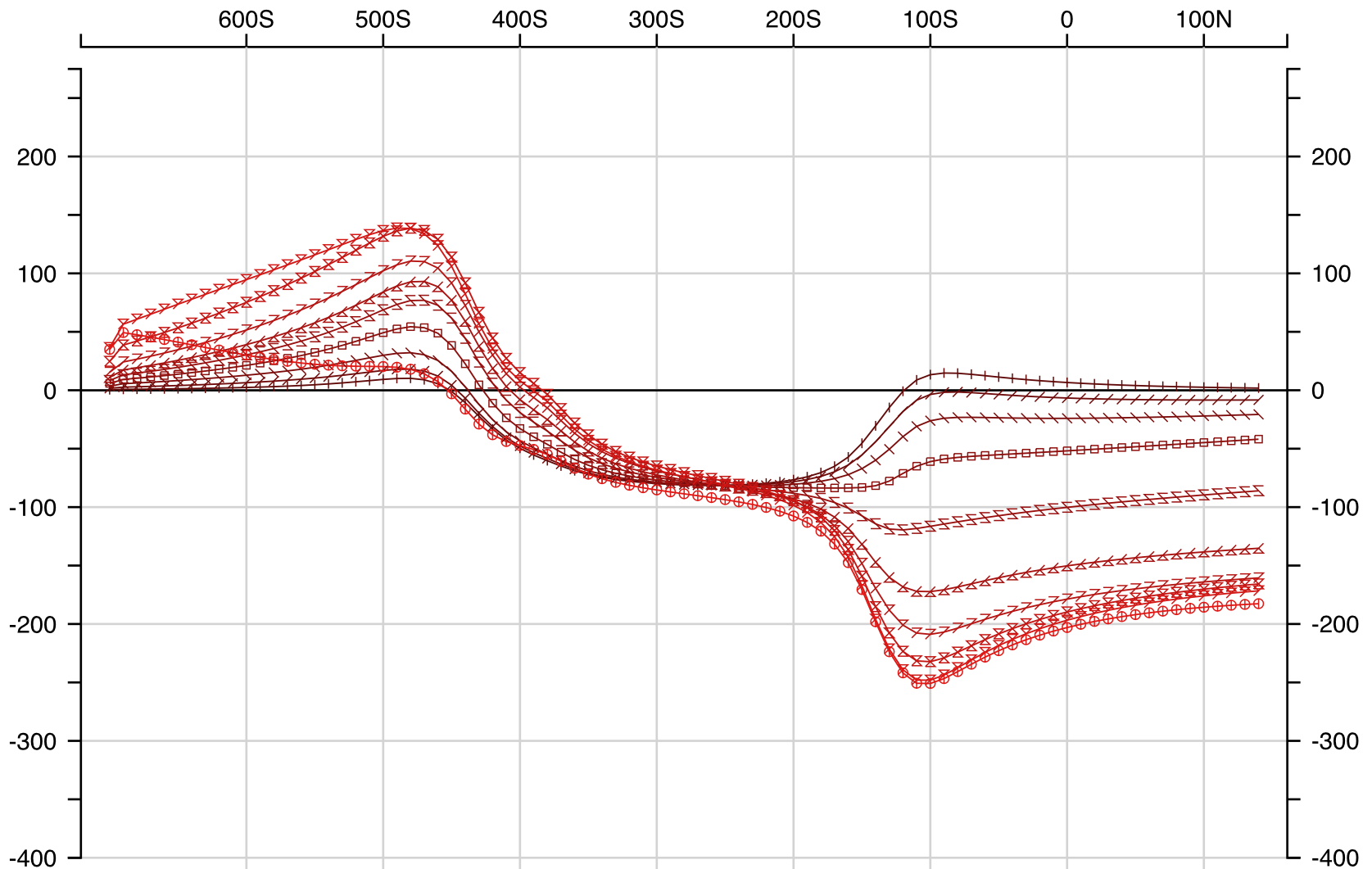
Ovoid + OverBurden + Dykes + Conduit Hz

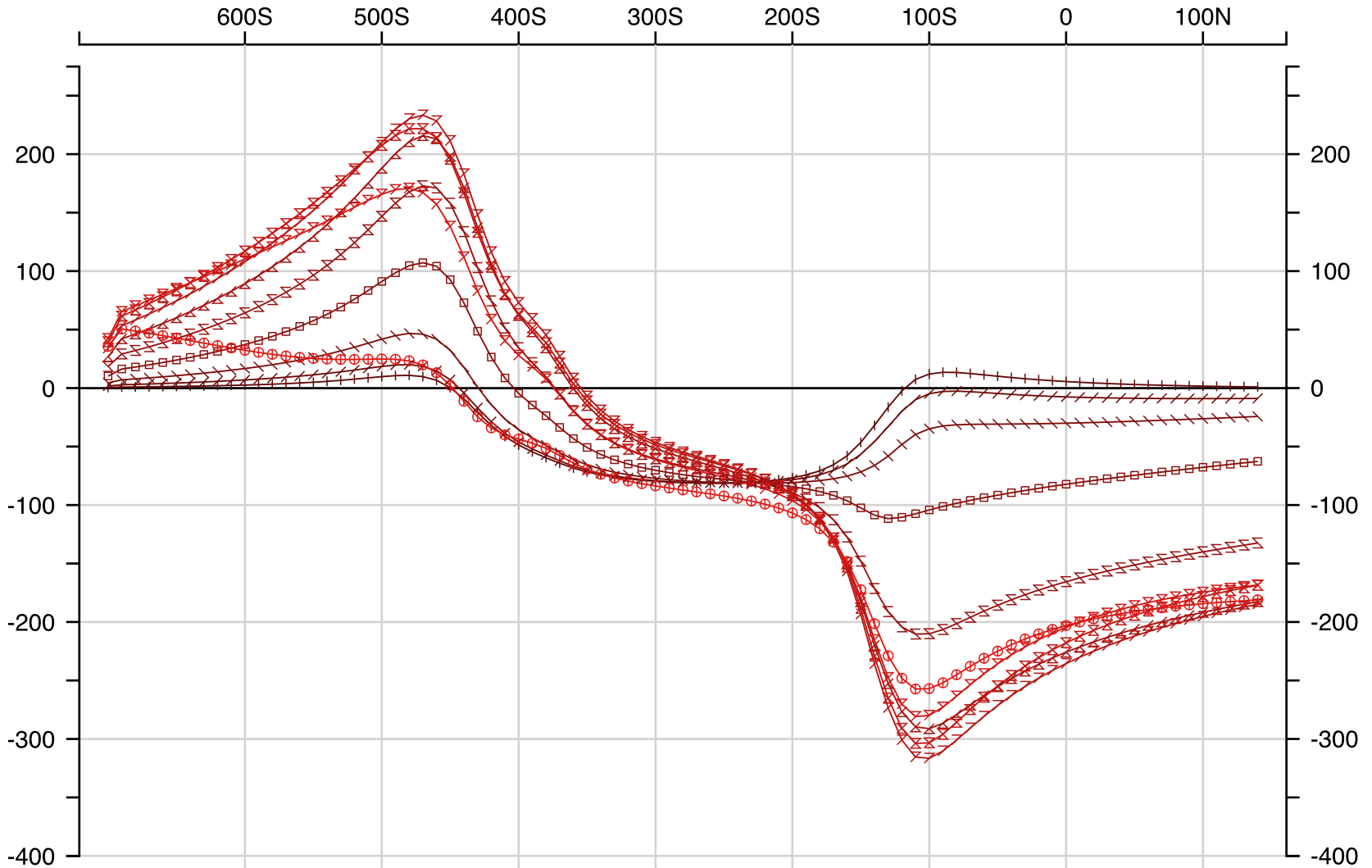
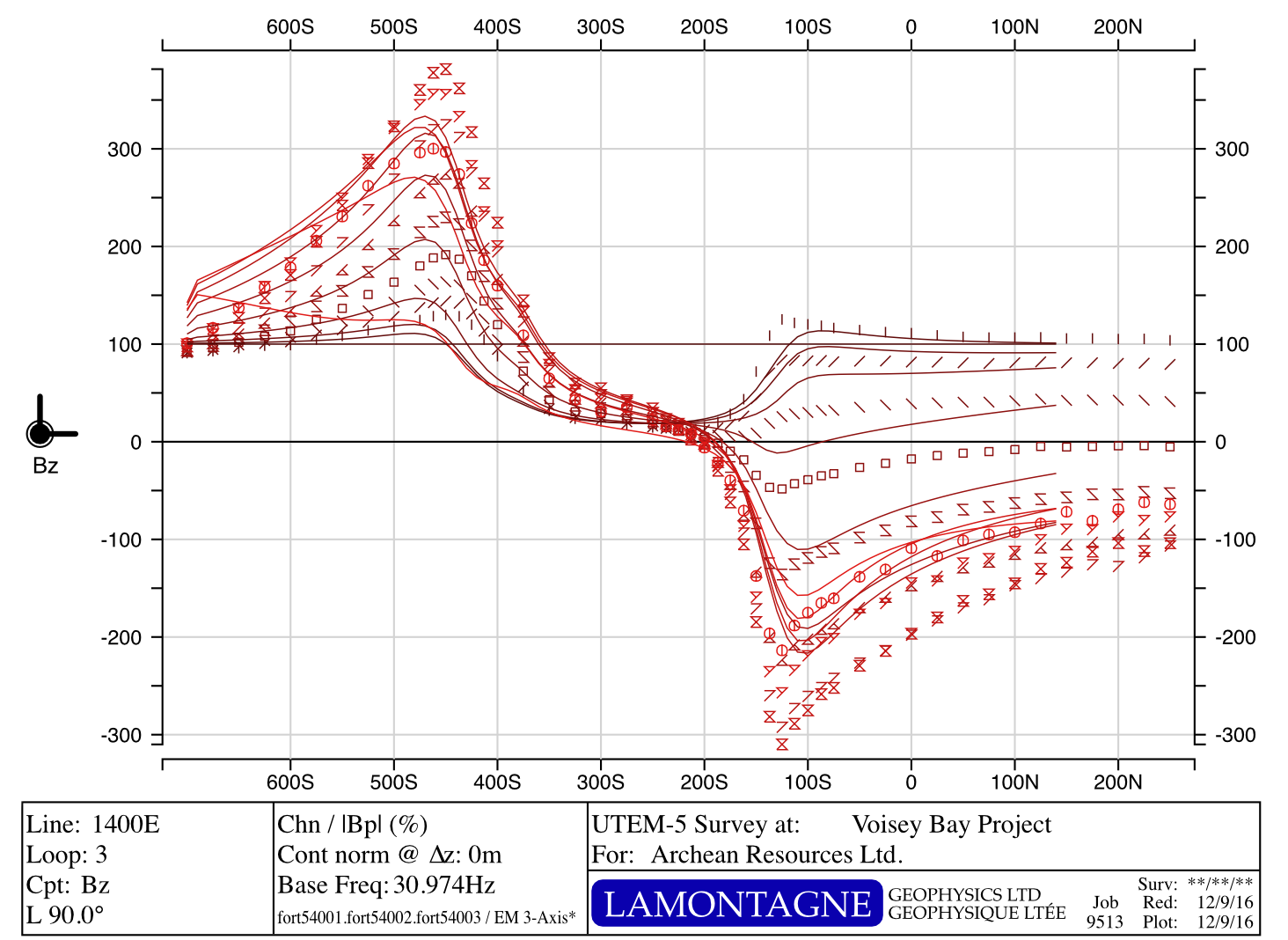
Ovoid + OverBurden Hx

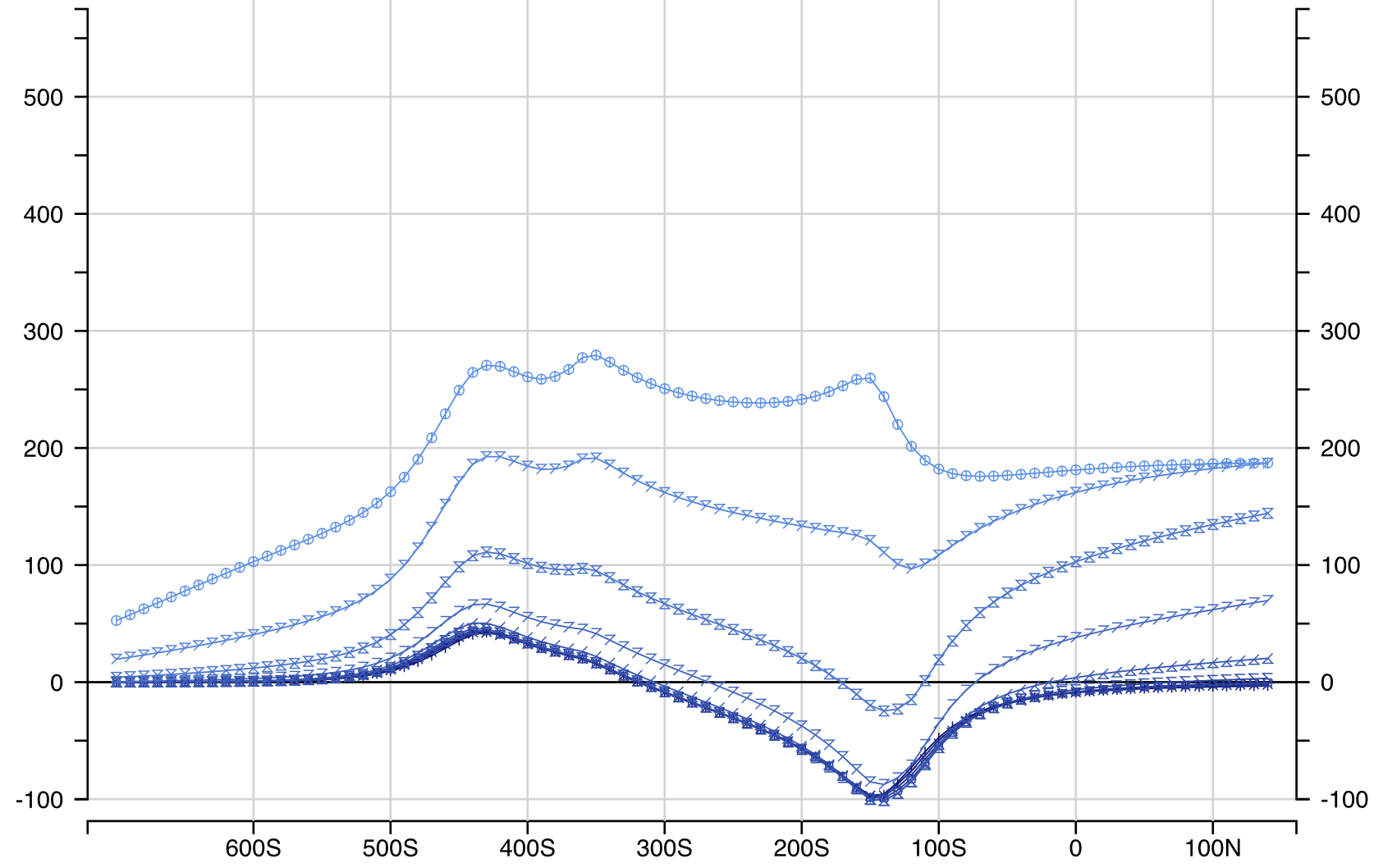
Ovoid + OverBurden + Dykes Hx

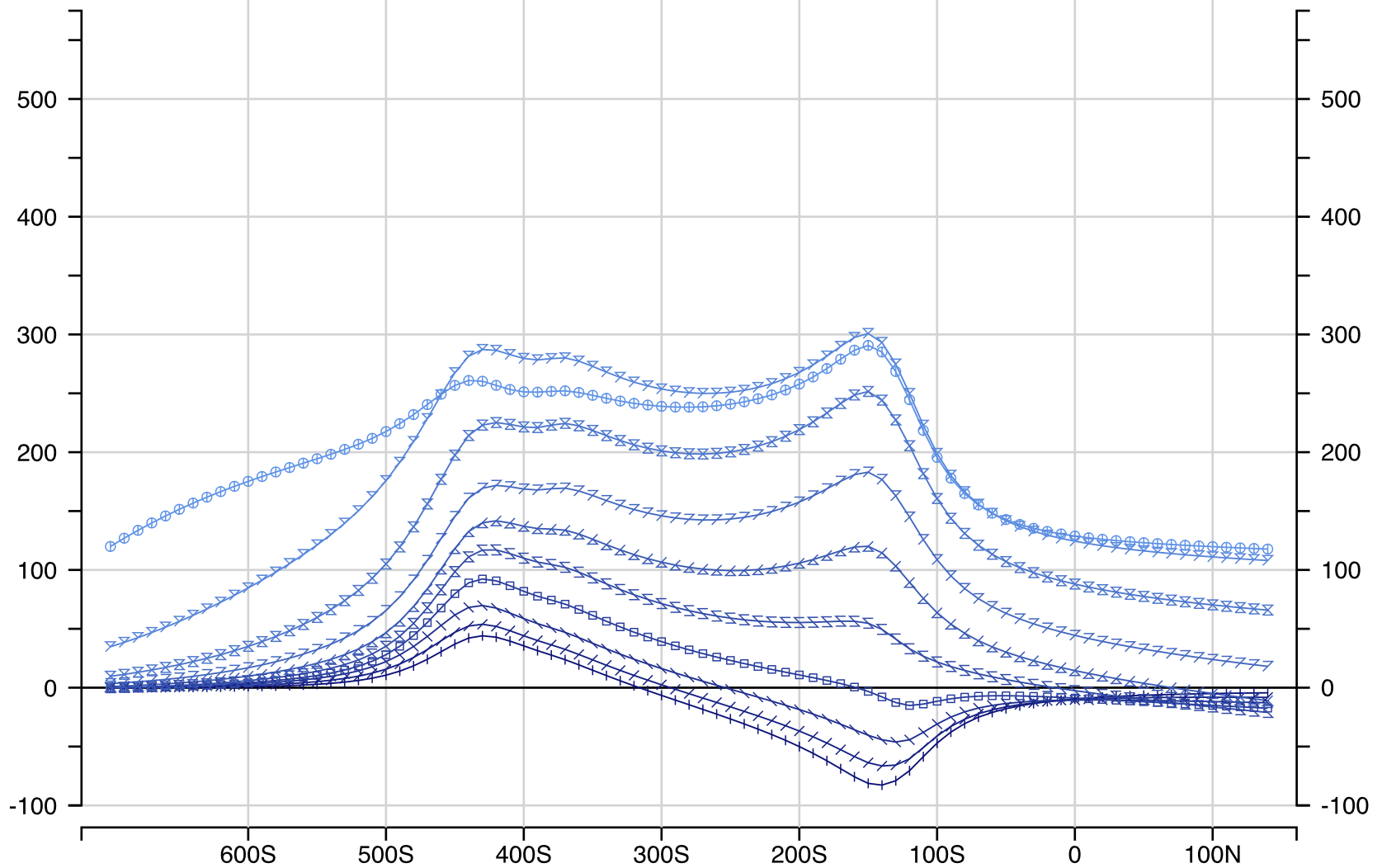
Ovoid + OverBurden + Dykes + Conduit Hx

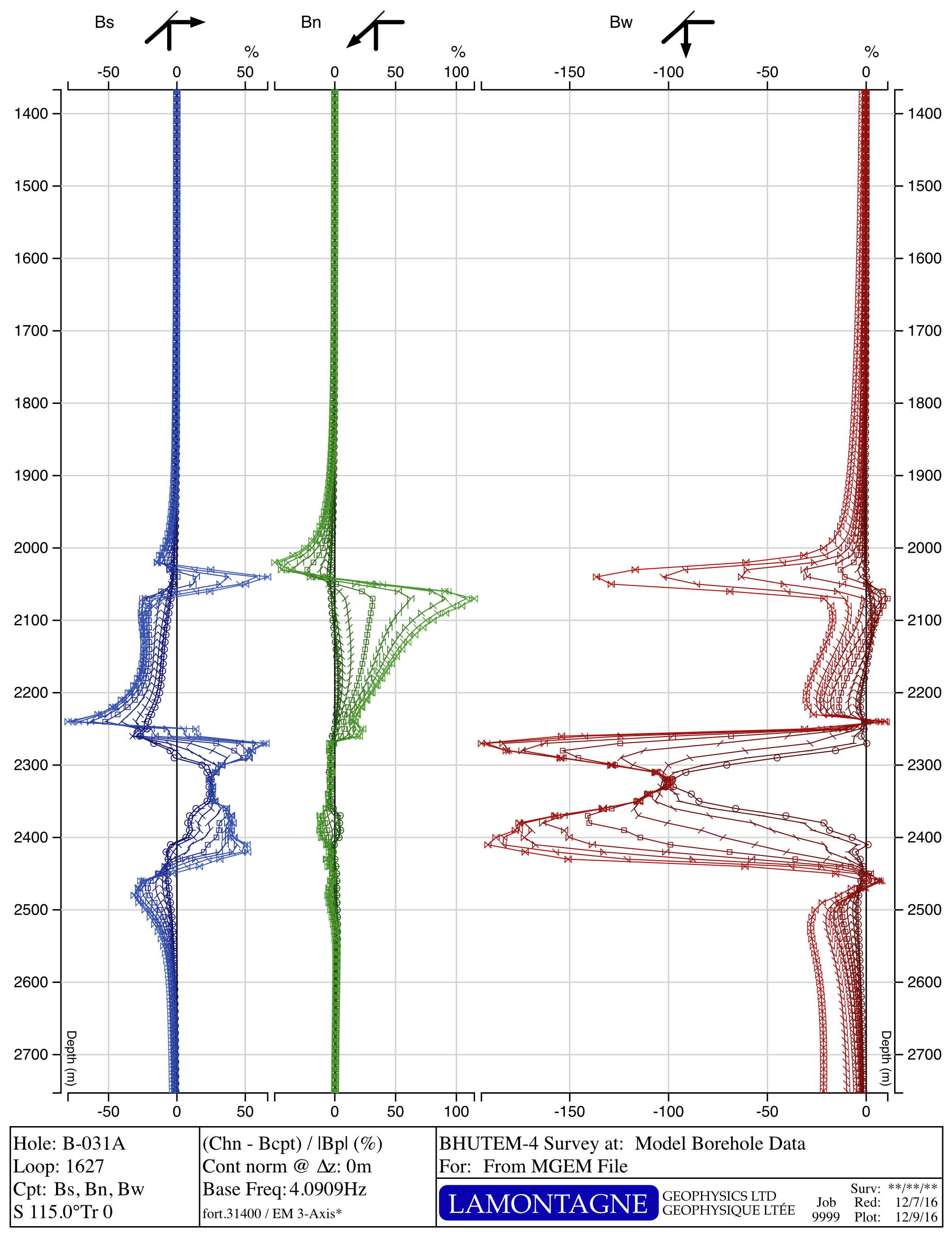
A More Realistic Exploration Example

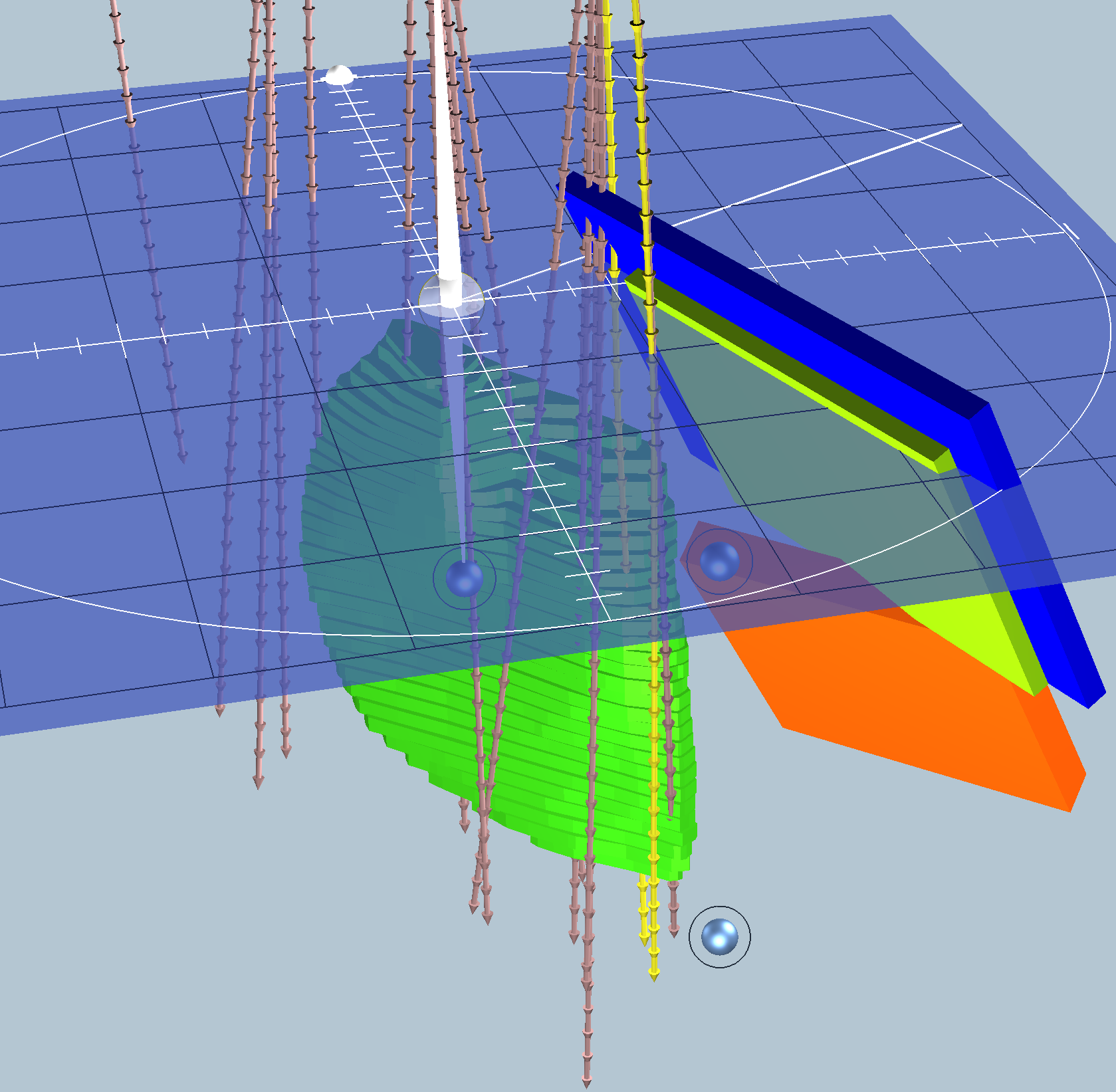
Thank You!